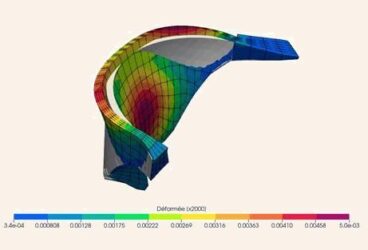
This article is aimed at engineers and focuses on the importance of predicting the concentration of mechanical stress and the practical need to reproduce this phenomenon through accurate computer simulations. Numerical experiments are conducted to verify that SimScale is able to reproduce the stress concentration as long as the mesh used at points of higher stress gradients is small enough to capture the phenomena.
Linear Elastic Analysis of Mechanical Stress Concentration in a Round Shaft
Three geometries or three different aspect ratios were considered. For each geometry, four different mesh sizes were used and, as a result, a total of twelve numerical simulations were carried out (see Figure 1). The diameter D is 0.02 m, the diameter d is 0.013333333 m and the radius of the shoulder depends on the r/d aspect used (0.15, 0.20,0.24). The flat face of the larger diameter side of the cylinder and the lower face of the cylinder is fully restricted, while the flat face on the smaller diameter side of the cylinder supports the application of a pressure load of 1e5Pa.
The elastic modulus and Poisson’s ratio used in the simulation correspond to a steel material. Default material properties are available on the SimScale platform. (Elastic Modulus E = 205 GPa and Poisson’s ratio = 0.28) .
The option tetrahedral with local refinement available on the SimScale CAE platform was used to refine the mesh around the shoulder fillet (see Figure 1). This option allows us to decrease the computing cost because the same accuracy is obtained with a minimum number of degrees of freedom. For example, a fine mesh is used where a strong variation of the gradient of displacement is present around the hole. Linear tetrahedral finite elements were used in the simulations.
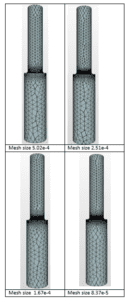

D/d = 1.5 and r/d=0.24
| Mesh size (m) | Number of nodes | Number of elements | Stress yy (Pa) |
| 5.02e-4 | 5257 | 21367 | 1.501e5 |
| 2.51e-4 | 13822 | 56596 | 1.564e5 |
| 1.67e-4 | 26151 | 105820 | 1.589e5 |
| 8.37e-5 | 76897 | 285351 | 1.606e5 |
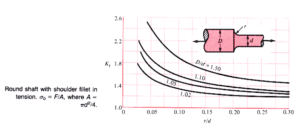
For an aspect ratio r/d = 0.24, the theoretical value of the mechanical stress concentration factor K_t is 1.6 and the stress predicted using the theoretical stress concentration factor (K_t) is 1.6e5 Pa. The predicted value of K_t using the numerical simulation is 1.6. It is important to note that the predicted value of K_t is calculated with the maximum stress obtained in the same direction of the applied pressure, which means the maximum stress in the y-direction).
D/d = 1.5 and r/d=0.20
| Mesh size (m) | Number of nodes | Number of elements | Stress yy (Pa) |
| 5.02e-4 | 5063 | 21587 | 1.56e5 |
| 2.51e-4 | 13626 | 59533 | 1.62e5 |
| 1.67e-4 | 31279 | 152852 | 1.68e5 |
| 8.37e-5 | 74379 | 302423 | 1.69e5 |
For an aspect ratio r/d = 0.20, the theoretical value of the stress concentration factor K_t is 1.7 and the stress predicted using the theoretical stress concentration factor (K_t) is 1.7e5 Pa. The predicted value of K_t using the numerical simulation is 1.69.
D/d = 1.5 and r/d=0.15
| Mesh size (m) | Number of nodes | Number of elements | Stress yy (Pa) |
| 5.02e-4 | 6190 | 31010 | 1.655e8 |
| 2.51e-4 | 13365 | 61566 | 1.781e5 |
| 1.67e-4 | 24402 | 112411 | 1.816e5 |
| 8.37e-5 | 65992 | 286383 | 1.827e5 |
For an aspect ratio r/d = 0.15, the theoretical value of the stress concentration factor K_t is 1.8 and the stress predicted using the theoretical stress concentration factor (K_t) is 1.8e5 Pa. The predicted value of K_t using the numerical simulation is 1.827.
The results presented above show the convergence of the stress yy with the decreasing of the mesh size around the shoulder (the place where the variation of gradients of displacements is significant) for the three different aspect ratios. They also include the expected convergence of results with mesh refinement that is typical in finite element analysis. The use of a bad design mesh in a problem where stress concentration is present could imply an over or under predict of the maximum stress within a structure, which results in an over cost in the design or a failure in service of the designed structure.
The results also show that the SimScale CAE platform was able to accurately predict the mechanical stress concentration in our round shaft with shoulder fillet in tension.
Simulmax helps companies develop physical models and simulations of their products, systems, and processes for design, improvement, and optimization with the aid of computer tools. The domains can be structural, thermal, fluid flow or a combination of them. Learn how you can collaborate.
SimScale’s CEO David Heiny tests the capabilities of the platform to solve a real-life engineering problem. Fill in the form and watch this free webinar to learn more!