A typical engineering design involves the prediction of deflections/displacements, stresses, natural frequencies, temperature distributions, etc. These parameters are used to iterate on material parameters and/or geometry to optimize their behavior. Traditional methods, like hand calculations, involved the idealization of physical models using simple equations to obtain solutions. However, these approximations oversimplify the problem, and an analytical solution can only provide conservative estimates. Alternatively, FEM and other numerical methods are meant to provide an engineering analysis that takes into account much greater detail—something that would be impractical with hand calculations. FEM divides the body into smaller pieces, enforcing continuity of displacements along these element boundaries. More information on “how FEM works” and “how to learn FEM” can be found in the respective SimScale articles.
Convergence in FEA What is Convergence in Finite Element Analysis (FEA)?
For those using finite element analysis, the term “convergence” is often used. Most linear problems do not need an iterative solution procedure. Mesh convergence is an important issue that needs to be addressed. Additionally, in nonlinear problems, convergence in the iteration procedure also needs to be considered. So, what does this mean? In this article, we investigate and address issues related to this term.
Convergence in FEA Mesh Convergence: h- and p-refinement in Finite Element Analysis
One of the most overlooked issues in computational mechanics that affects accuracy is mesh convergence. This is related to how small the elements need to be to ensure that the results of the finite element analysis are not affected by changing the size of the mesh.
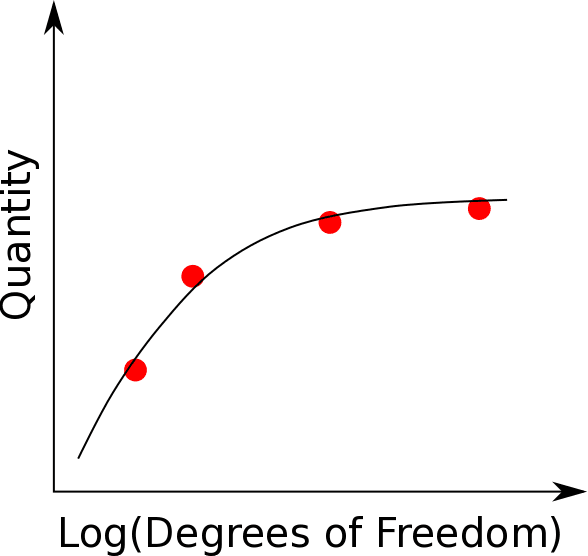
As shown in Fig. 01, it is critical to first identify the quantity of interest. At least three points need to be considered, and as the mesh density increases, the quantity of interest starts to converge to a particular value. If two subsequent mesh refinements do not change the result substantially, then one can assume that the result has converged.
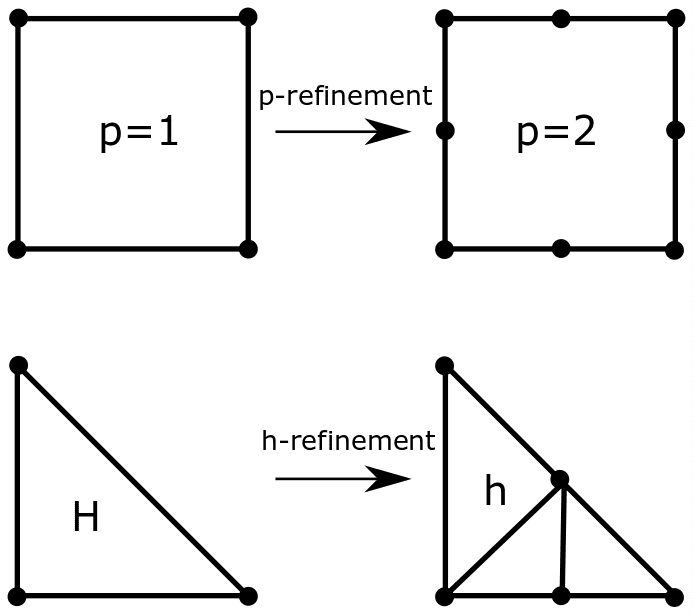
Going into the question of mesh refinement, it is not always necessary for the mesh in the entire model to be refined. Saint-Venant’s Principle enforces that the local stresses in one region do not affect the stresses elsewhere. Hence, from a physical point of view, the model can be refined only in particular regions of interest and further have a transition zone from a coarse to a fine mesh. There are two types of refinements (h- and p-refinement), as shown in Fig. 02. H-refinement relates to the reduction in the element sizes, while p-refinement relates to increasing the order of the element.
However, it is important to distinguish between the geometric effect and mesh convergence. Particularly when meshing a curved surface using straight (or linear) elements, which will require more elements (or otherwise mesh refinement) to capture the boundary exactly. As shown in Fig. 03, mesh refinement leads to a significant reduction in errors.
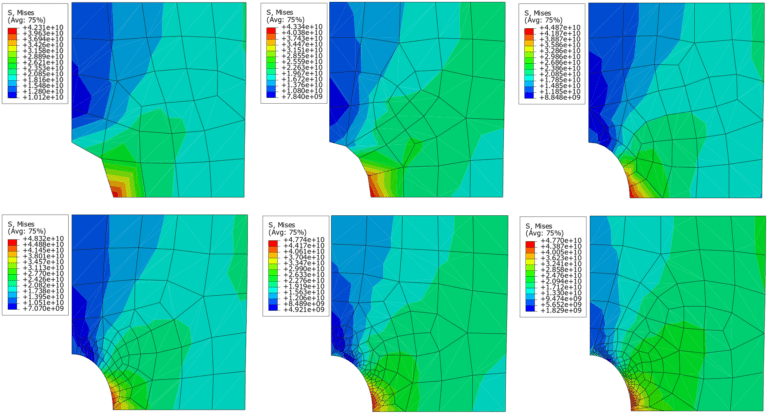
Such a refinement can allow an increase in the convergence of solutions without increasing the size of the overall problem being solved.
FEA Convergence in Presence of Singularities
After reading the above section, it feels safe to assume that once the stress converges in a particular part of the structure, using the same element size elsewhere should lead to converged solutions. However, this is not a valid assumption.
Most models have corners, both internal and external, where the radius is assumed to be zero. This is also the case in the presence of cracks. In these instances, the stresses are theoretically infinite. Now can you guess why airplane windows do not have corners but are rounded at the edges?
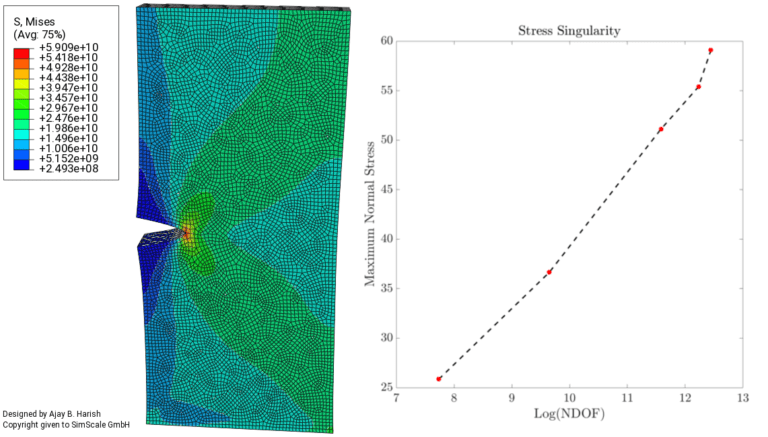
In the presence of the singularity, the mesh needs to be refined around it. However, as shown in Fig. 04, the more the mesh is refined, the more the stress continues to increase and tend towards infinity.
Hence, in the presence of fillets, it is generally more reasonable to assume an actual radius and then refine the region using a sufficient number of elements. For more details on mesh singularities, we recommend our recent article on the SimScale blog titled “Mesh Size Influence on Mechanical Stress Concentration”.
Finite Element Analysis Convergence During Locking
Another commonly encountered nonlinear problem relates to locking—namely, the volumetric and shear locking effects. Volumetric locking is commonly encountered in problems related to incompressibility in hyperelasticity and plasticity problems. Alternatively, shear locking is generally encountered in bending-dominated problems.
For more discussion on volumetric and shear locking, you can refer to our articles on the SimScale blog: “Modeling Elastomers” and “Meshing in FEM” respectively.
Fig. 05 shows a standard problem in testing incompressible effects. As shown, a small pipe with internal pressure is considered. Such applications are commonly found in various environments, including human arteries. Only a quarter of the model needs to be considered due to the symmetry in the problem. As the Poisson ratio tends to 0.5, the bulk modulus tends toward infinity, and thus the material demonstrates incompressibility. In this instance, second-order elements are preferred or, in other words, a p-refinement is required. The figure also illustrates the behavior of different element types with an increase in the Poisson ratio.

Similarly, Fig. 06 shows a simple beam-bending problem where a moment is being applied on the free end. The deflection at the free end of the beam is considered, and this problem even has an analytical solution for comparison. Fig. 06 shows the convergence of the deflection for different kinds of elements.
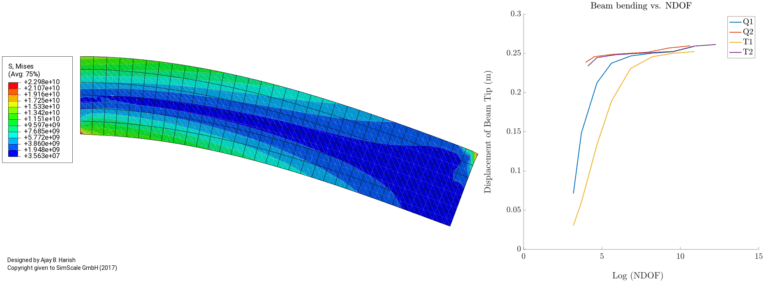
FEA Convergence How to Measure Convergence
So now that the importance of convergence has been discussed, how can it be measured? What is a quantitative measure for convergence? One way to measure it would be to compare with analytical solutions or experimental results.

As shown in Fig. 07, several errors can be defined for displacement, strains, and stresses. These errors could be used for comparison, and they would need to reduce with mesh refinement. However, in a FEM mesh, the quantities are calculated at various points (nodal and Gauss). In this case, where and at how many points should the error be calculated?
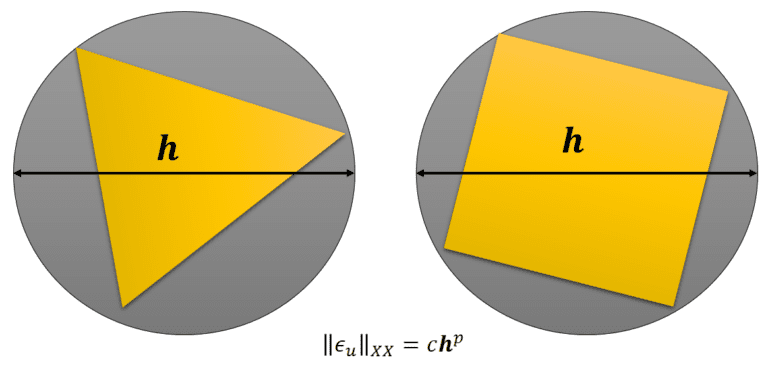
Alternatively, norms are defined such that the averaged errors over the entire structure or part of the structure can be calculated. As shown in Fig. 08, the error norms can also be compared to the size of the element. Here “c” is a constant of proportionality, while “h” is the element size, as defined in Fig. 08. Hence, several errors such as L2 and energy error norms can be defined as below:
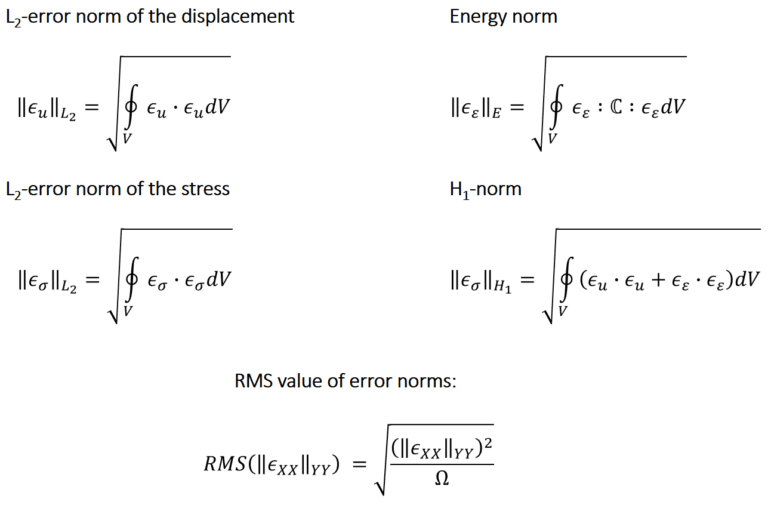
However, in real practical applications, a non-dimensional version of the same is more useful to assess the actual degree of error. Therefore, in this instance, the root-mean-square value of the norms, as defined below, is used to plot the reduction in error.

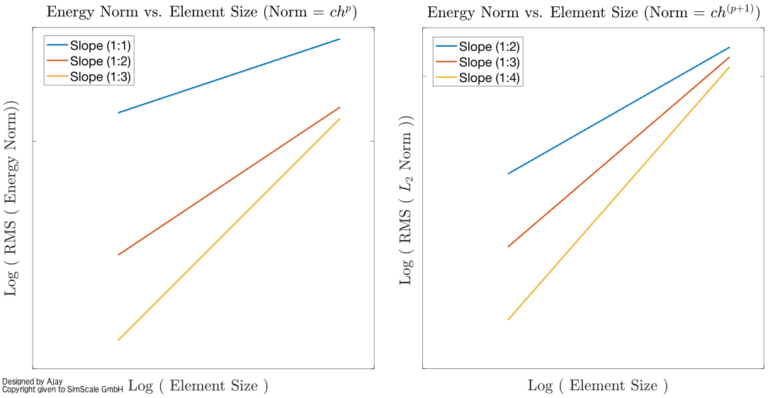
The final topic is related to the rates at which these errors ideally decrease. If we are using linear or quadratic or cubic elements, how does one judge whether the error is decreasing at the right speed or the quality of the algorithms coded? As shown in Fig. 09, the L2-norm error decreases at the rate of p+1 and energy-norm at the rate of p.
Convergence in FEA Conclusion
I hope this article has given a comprehensive overview of convergence, convergence rates, and ways to accurately judge these aspects in a finite element analysis. Convergence plays an important role in the accuracy of solutions obtained using numerical techniques like FEA and thus needs to be comprehensively analyzed in any given problem.
Learn how to get easy access to cloud-based tools for CAD and simulation by watching the recording of the webinar “How to Optimize Medical Devices with Cloud-Based Simulation” in partnership with Onshape. All you need to do is fill out this short form, and it will play automatically.


