Elastostatics
The momentum balance is given by
In this case \underline{\underline{\sigma}} is the Cauchy stress tensor, \underline{b} the body force density and \underline{u} the field size we need: the displacement vector.
In the case of quasi-static processes we can say that \lvert \rho\ddot{u} \rvert\approx \underline{\underline{0}} .
With the equation above we get the following equation:
To solve this problem, we need boundary conditions (BC)!
In the case of elastostatics we need so called Dirichlet (essential boundary conditions) boundary conditions and Neumann (natural boundary conditions) boundary conditions:
Excursus
These two boundary conditions have to be disjoint sets. That means that there is no intersection between the boundaries and they have no element in common (no intersection). Well what does that mean in case of elastostatics? Traction and displacement both cannot be prescribed at the same boundary point! We write this as
We have natural as well as essential boundary conditions as mentioned above. Essential boundary conditions are the ones that are imposed EXPLICITLY on the solution whereas natural boundary conditions are the ones that are consequently satisfied after a solution of the problem has been achieved. Please be careful with the definition of Dirichlet = essential and Neumann = natural!
There are cases where the Dirichlet BC can become a natural BC (Nitsche’s method \rightarrow related to discontinuous Galerkin method) and Neumann BC can be transformed into an essential condition using the so called mixed methods. But for our “Beginner’s course” we can assume that the Dirichlet BC is an essential BC and the Neumannn a natural one.
Any boundary is either an essential of natural boundary and their union is the entire boundary.
Mathematically, we can write the following:
The two boundaries are complementary which means that the essential boundary and its complement, the natural boundary, constitute the total boundary and vice versa.
To be completely defined we need a constitutive law which is in case of a geometric linear perspective a function of an infinitesimal distortion
In linear elasticity theory, we have the generalized Hooke’s law
where \mathbb{C} defines the positive definite stiffness tensor of the material.
Heat conduction
The heat conduction equation for transient problems is
Where \rho is the mass density, \theta the temperature, h the applied heat , c the specific heat capacity and \underline{q} the heat flow vector.
As in elastostatics we also need boundary conditions as well as initial conditions. The initial condition would be the temperature distribution \theta(\mathbf{x},t=t_0) within our component at the beginning of our process.
• Dirichlet-Boundary
Specifies the values that a solution needs to take on along the boundary of the domain. Normally we prescribe the field size we are looking for
• Neumann-Boundary
It specifies the values that the derivative of a solution is to take on the boundary of the domain. Normally we prescribe the normal derivative of the flux (in heat conduction it is the heat flux)
• Robin-Boundary
It is a specification of a linear combination of the values of a function and the values of its derivative on the boundary of the domain. The Robin-Boundary depends on the solution variable
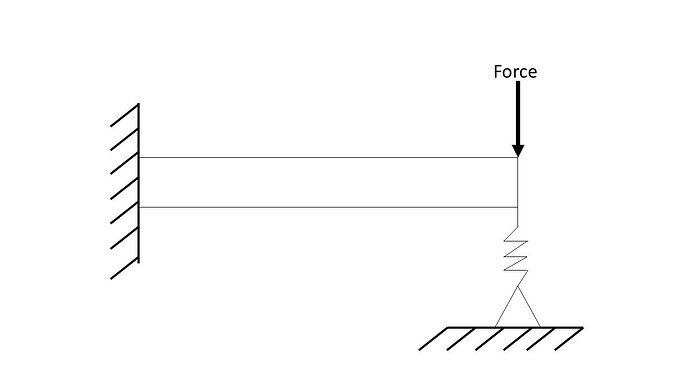
An example for heat conduction would be convection. In terms of elastostatics we would have something like an elastic bedding that looks like this:
As previously mentioned in the excursus the different boundaries together form the whole boundary \Gamma = \partial\Omega = \Gamma_\theta \cap \Gamma_q \cap \Gamma_r.
Heat sources can be at the boundary of the body (\Gamma_q) or heat sources can occur in the form of an applied heat h (hot stone in cold water). Also keep in mind what we said about the boundaries on one point: ONLY ONE AT A TIME \rightarrow disjoint sets
Our life will be much easier if we look at the steady-state head conduction.
The heat conduction equation from the beginning simplifies because \dot{\theta} \approx 0.
As in elastostatics we need a constitutive law which is Fourier’s Law of Heat Conduction.
\mathbf{\kappa}(\mathbf{x}) is the thermal conductivity in tensor notation.
Why is there a minus in front of the \kappa ? Because the heat flux is directed opposite to the temperature gradient (“From warm to cold”).
Sources:
• A First Course in Finite Elements by Jacob Fish and Ted Belytschko (See also \rightarrow What do I recommend)
• ROBIN BC
• NEUMANN BC
• DIRICHLET BC
• Lectures of KIT Karlsruhe (Script: Einführung in die Finite Elemente Methode Sommersemester 2014)
• Essential and natural BC
This was the second part for FEM fundamentals. The following chapter will provide a review of basic matrix algebra.
If you find any mistakes or have wishes for the next chapters please let me know.
First chapter: The Finite Element Method - Fundamentals - Introduction [1]