To answer the questions from @mas985:
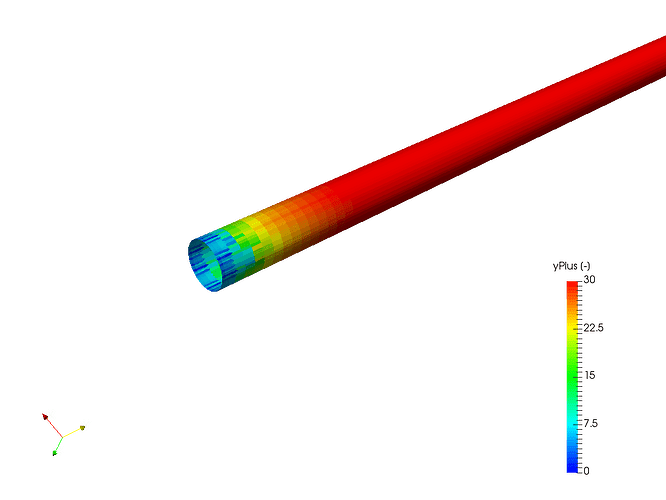
I get a y+=1 of 1.4e-5 m and y+=30 of 4.2e-4 m. Since this represents the cell center, the cell width should be twice this value or 2.8e-5m (0.028mm) for the resolved case and 8.4e-4m (0.84 mm) for the wall function case. When I did a yPlus output plot for your wall function case, it was around 20 which is to be expected given the above calculation.
How did you come to your values and why are your two values for the two cases not a ratio of 30 (y+ 1:30)? The wall function case obviously yields the correct results even though the y+ value is less than 30 but I thought that was a no no according to other SimScale documentation.
I see that the documentation did not explain well enough how we arrived to those values and which choices we made in the process. The target wall spacing was calculated with expressions similar to those you were using, but the difficulty with “wall function” approach and this particular case is that flow velocity is relatively low which makes boundary layers thick and, ultimately, the necessary first cell height for y+ = 30 relatively large (1/10 of the diameter). Satisfying the condition of high yPlus is not possible without severely coarsening the mesh. At that moment we decided not to coarsen the mesh any further and the result was a mesh with incorrect y+ values. Nonetheless, the results showed robustness towards non-ideal wall spacing, especially for kOmegaSST turbulence model which is known to give accurate results for yPlus being well below 30, because of the blending functions it is using. Regardless of that, one should always try to achieve the recommended average yPlus higher than 30 in most of the domain, so I created a mesh which does that. With this new mesh you can see that results of pressure drop for kEpsilon are significantly improved. There is a trade-off, however: as mentioned earlier, such a coarse mesh near the wall doesn’t capture the velocity profile very well. The corresponding documentation page will soon be updated with the results obtained with the new mesh.
… the meshes were imported into the validation project so there is no documentation on exactly how they were created. Can this be added to the project?
Meshes from the old validation projects were just imported to the new one. Since some valuable information on meshing settings is lost in this way, as you correctly pointed out, I updated the project to include the mesh creation step.
My second question is around the initial conditions of k and omega. Looking at the average output face values of k & omega, they are quite a bit larger than the initial conditions. I am assuming this is because of the fully developed flow so I was wondering if there is a way to determine fully developed exit values for k & omega and would it not better to use those as inputs?
Prescribing turbulent BCs is often very tricky and one of the difficulties of turbulence modeling. For fully-developed pipe flow, you would ideally prescribe profiles of all flow quantities at the inlet, including those which model turbulence (k, epsilon, omega…). For some cases, including duct and pipe flows where accurate profiles of turbulence quantities are unknown, it is acceptable to specify uniform values, while being aware that flow needs to develop inside of the domain. For external flows, constant values are appropriate if the boundary is far enough from the object of analysis.
If you look at the expressions used to estimate inlet k and omega/epsilon in the validation page you will see that the value of turbulence intensity is the basis for their calculation. For most industrial cases, turbulence intensity is hard to know without experimental data, so it is usually heuristically assumed to be in range of 2-15%. For pipe flow, on the other hand, the expression I = 0.16Re^(−1/8) is commonly used, as it was in this study. This empirically derived expression estimates the turbulence intensity at the core of a fully-developed duct flow. One more common assumption is made here, that the turbulence length scale is 7% of the hydraulic diameter. Regardless of the many unknowns in the face of this problem kEpsilon and kOmegaSST models are usually robust in regards to variation of prescribed turbulence quantities the inlet. However, if a gross mis-estimation is introduced, it will be clear form lack of convergence and nonphysical nature of results.