i m used to steady-state CFD, which works nicely in my case. But i need to do transient simulation. It diverges all the time. I tryed “delta t” to set 0,1; 0,05; 0,01; 0,00005 it failed in all cases. If i set run to steady-state it converges nicely.
Any ideas what i have done wrong ? ( simulation is CFD of half-aicraft in 16m/s)
Hi @Novak_Ondrej!
Please share the project link with us as well to have a look at it. Are you really trying to simulate such a low velocity?
Cheers,
Jousef
Yes, velocity is correct. Simulation should analize stall and fall of aircraft at low speeds
Hi @Novak_Ondrej!
If you perform a steady-state simulation CFL is not involved in your simulation. Now when you switch to transient CFL has to be taken into account and according to your cell size the CFL condition has to be chosen wisely and should be smaller than 1 but can in some cases be bigger than one.
Good blog post about that topic: CFL Condition
In general:
Regarding your mesh I would still increase the domain size, as a template you can have a look at this project: Aerodynamics of Commercial Aircraft. And for the wall functions we will have to see in which range the y-plus value is to see if we would have to adapt the inflated boundary layer cells.
Let me know if you have any further questions. My colleagues @Get_Barried, @vgon_alves and I would be more than happy to help you out!
Best,
Jousef
Thanks. I understood that i have lower time step or make mesh more coarse.
Making mesh more coarse should be neccessary.
I tryed lowering time step to e-9 a it did not help. Simulation crashes when max courant number is 14. Why is that ? e-9 is really small time step.
Should i try making it even lower ? There must be other error
Hey @Novak_Ondrej!
I actually meant to make the mesh way finer and the domain bigger! If you have a coarse mesh and a small time step the CFL number is tending to zero. Use the template I posted as a rough estimate for your domain size and make the mesh finer as previously mentioned.
Cheers,
Jousef
I did not follow your instructions and i tryed more coarse mesh and found sth. , the air flowing at 34000 m/s.
So i checked all simulations i did before, just before they failed. Found that even though i set flow at 16m/s air is flowing inside domain at speeds around 100m/s. This explains why lowering time step does not help. There must be reason why simulation ramps up the speed to such high levels.
Any ideas ?
That’s exactly the problem. You have to decrease the cell size or if you want to put it in other terms increase the finenessto avoid such unphysical behavior. Maybe @Get_Barried and @vgon_alves can help here and assure you that a coarse mesh is not going to get you anywhere if it is “too coarse” as in your case.
Cheers,
Jousef
Hi @Novak_Ondrej,
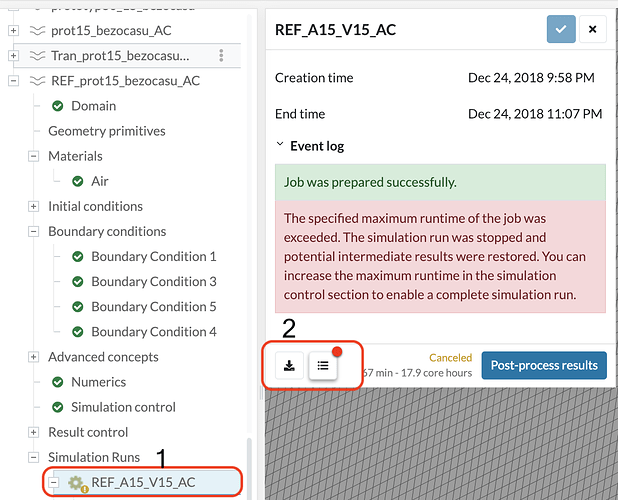
Before I get into CFL and all that, your mesh may have some quality issues. I see you have adjusted the quality controls and the mesher may not deem some cells as illegal where in fact they are or at least of very very low quality which may kill your simulation. You might want to set the settings back to default and remesh the geometry to see where the problematic areas lie so you can refine or adjust them in CAD. Refer to the figure below.
So for starters lets look at the required end time of the simulation. For transient simulations, “time” does exist so we need to consider how long the medium takes to progress through the domain. Finding this out is simple, just take your distance (maximum distance in the domain of the flow direction) divided by speed (which is your flow speed). For your case (simulation Tran_prot15_bezocasu_AC), that would be 50 m divided by 16 m/s which equals to 3.125s. So you at least need 3.125s end time to allow full flow progression through the domain. However, the simulation also has turbulence which you need to allow to kind of settle down before you call it day. This adds to your simulation time and is difficult to tell how much more time you actually need till at least you get your baseline simulation down (3.125s end time).
So considering that you’ve tried a 1E-9 timestep, you’re looking at over 3.125 billion iterations. That is, simply put, computationally wasteful.
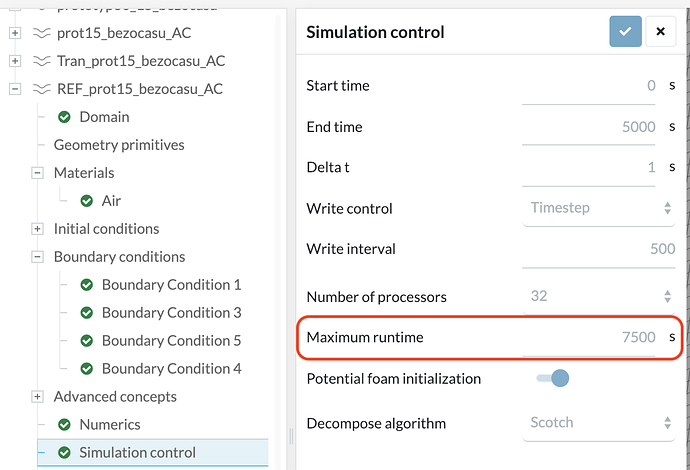
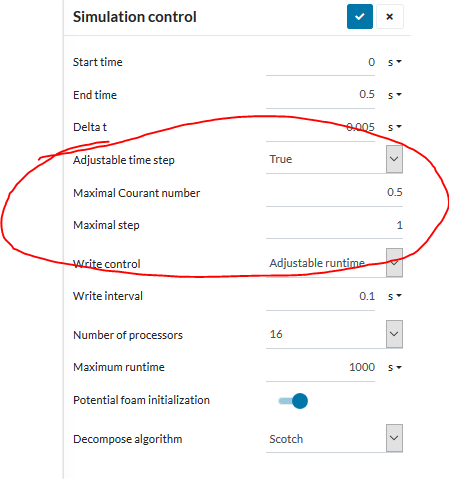
Now we need to adjust your CFL to have a good balance between time taken and not letting the simulation crash. For starters should try to keep your CFL below 1. The solver can adjust for this via the simulation controls automatically, increasing and decreasing timesteps as needed to keep the CFL below the set amount (in our case 1). Refer to the figure below to set this. Do note that however only the PIMPLE algorithm allows this adjustable CFL under the result control. Do ensure you leave all the settings at default for the numerics.
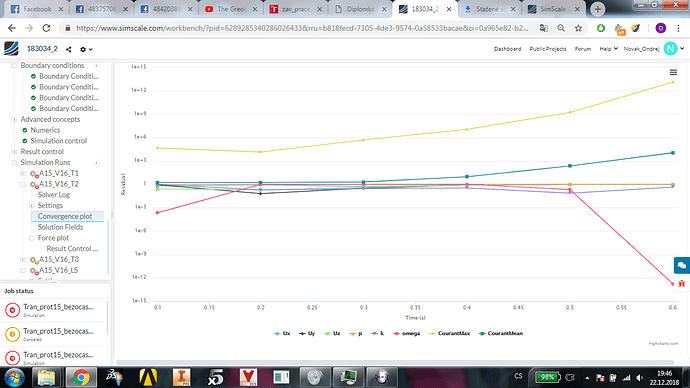
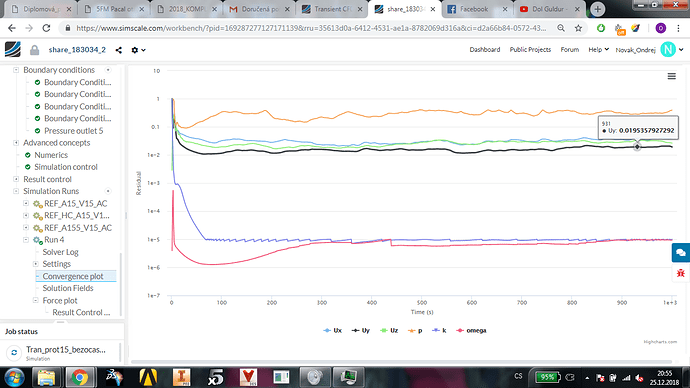
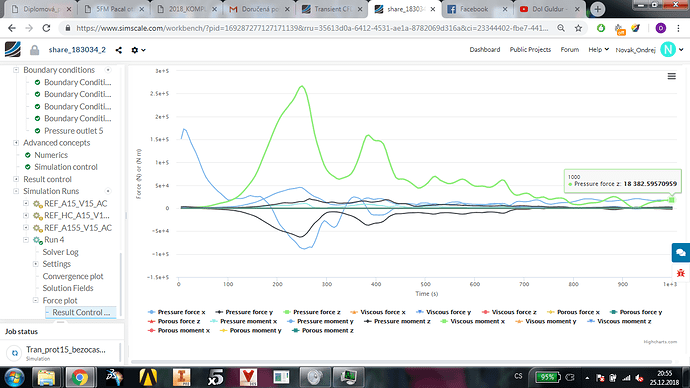
Go ahead and attempt to run the simulation and observe the timesteps in the convergence or result control plots. If you see it increasing by say 1E-3 then you’re home free as it only takes about 3000 ish iteraitons to complete. However, I do think based on what you’ve tried, you may not get so lucky.
@jousefm I’m a little confused. Based on the math of the CFL condition, assuming my CFL is fixed (1), a is fixed (16) and unknown is delta T, the larger/coarser the mesh for delta x, the larger the timestep that can be taken to maintain below the CFL value no? So technically, a coarser mesh should be more able to run. The only issue I see with a coarser mesh @Novak_Ondrej would relate back to what I’ve first mentioned where your mesh quality is insufficient, causing your simulation crash due to divergence rather than a CFL value that is too high.
Assuming I’ve understood the CFL correctly, based on my visual estimates, for your largest cells, the timestep needed is < 0.025s (delta x = 0.4 m) and the smallest cell which is a semi-uninflated layer on your geometry, timestep needed is < 5E-7 (delta x = 8E-6). But if you use the PIMPLE algorithm instead, then you don’t have to worry about the timestep as the solver automatically adjusts for you.
Also the good thing about the PIMPLE is that once you’ve settled all your mesh quality and any quirks in the simulation, you can use a CFL beyond one as shown in this post here. Note that PIMPLE is the only algorithm available now to be able to take advantage of this.
Hope this helps.
Cheers.
Regards,
Barry
Hi Barry!
Indeed one might argue that a coarse mesh will be better and indeed it is depending on what you define as coarse - too coarse will definitely make some problems and may not even converge. Additionally a too fine mesh will probably have problems with the Péclet number rather than the CFL number introducing non-physical diffusion. And as correctly mentioned you can use the PIMPLE solver where you have the option to limit the time-step to a maximum CFL number and the solver choses one automatically.
Cheers,
Jousef
Thanks for response.
I tryed making better mesh. I used default settings for quality control a refinements ant other stuff from aircraft workshop here on simscale.
Transient simulation still diverges. It seems to me like the mesh is good enough. But there is no other error that mesh indentified. But what other than mesh could have gone wrong ?
Can you please check my mesh and make suggestions ( the last one called REF_40_A15) because i cant see any problem and according to those webinars, its perfectly ok, but the transient simulation still diverges.
Simulation converges when using steady-state.
Thanks a lot
Hi @Novak_Ondrej!
Are you referring to the simulation called “REF_prot15_bezocasu_AC”? If so then the convergence looks promosing but you have to increase your maximum runtime in the simulation control - the mesh looks “perfect” 
Attached some pictures for future simulations that can help you identify the problems easier.
\underline{\textbf{1. Where to find the problem?}}
You can click on the run (1) and then on the “message icon” (2).
We can see it tells us there is something wrong with the runtime.
\underline{\textbf{2. Where to increase the runtime?}}
You can type in a very big number (for instance 300,000) just to make sure your simulation does not stop in the first place or use the Run continuation which can be found in this post: Platform Update 12/2018
Cheers,
Jousef
I checked steady-state simulation and its fine, lift and drag values are perfect.
But this mesh still fails for transient simulation. It diverges. I used automatic timestep adjustement on this new mesh and it failed. I must have made misstake somewhere
Hi @Novak_Ondrej,
can you tell me which simulation you are referring to? I thought it is the last one in your tree. Give me the name and I will check it out.
Cheers,
Jousef
REF_prot15_bezocasu_AC - this one is steady-state. It works fine with old mesh and a bit better with new one
Tran_prot15_bezocasu_AC - this one is transient. It does not work with old mesh and neither with new one
The transient one is problem. I tryed making better mesh and using timestep autoadjustment according to instructions here but it did not help.
Hi @Novak_Ondrej!
That’s related to the BC’s - I started a run a while ago and it is at 70% now, looks promising so far. Once it has finished I will share the new setup with you.
Cheers,
Jousef
Great ! nice to hear it works somehow
Are you sure its the right project ?
I can see you created simulation run. But its not transient, its steady state (Run 4). And its nowhere near converged. Lift force on that aircraft 18.3 kN ?
Maybe i m missing sth. but this is not correct at wall. I m trying to make transient simulation not steady state. Why your residuals are 0,3 ? it should be under 1E-3
