Hi everyone,
I am modelling a complex geometry (pseudo-fractal) in a rectangular computational domain: SimScale Login (for some reason the link does not seem to work).
I am using a K-omega SST model but I have a question. For flow around an obstacle, the critical Re is around 30000; For flow over a wall/flat plate, the critical Re is around 500000. Setting the L (characteristic length) in the Re formula to the length of my geometries (0.05m-0.3m) or even to the thickness of the flow (0.4m) results in flows below the turbulence onset threshold. So it suggests that the flow should be laminar.
However, I have checked the velocity profile of the flow (K-omega SST model) by the time it encounters the obstacle and it affirms the logarithmic law of the wall indicating a perfectly developed turbulent flow. How does this work? Can anyone help?
Cheers,
Daniel
Hi @dperez_pinedo, thanks a lot for posting at our forum 
Regarding the following part of your post:
Unfortunately SimScale does not support a model which takes into account the transition between laminar/turbulent flow, so that this result is expected.
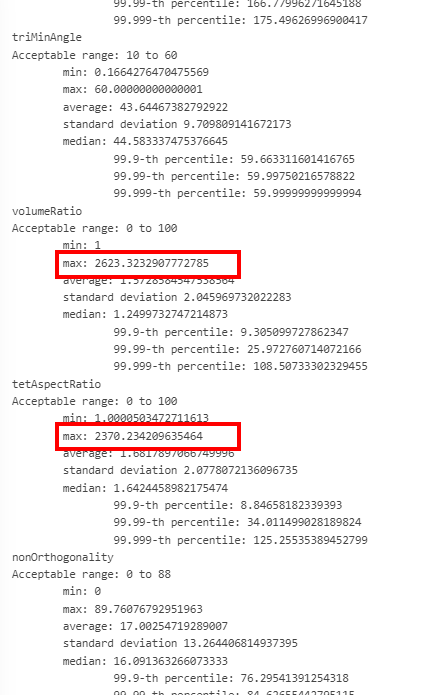
However, there seems to be some issues with the quality of your mesh:
The workflow to inspect that can be found here.
That might be due to the model you’re trying to simulate, which have really small edges that would make it difficult for the mesh to be adapted to:
An alternative would be for the small object to be modelled as a flat surface with a defined roughness (refer to this knowledge base article). Is that an option?
I hope that helps!
Best,
Igor
Could you please expand on this? I am not too sure I understand how the flow can be turbulent with such low Re numbers.
Hi @dperez_pinedo, sure!
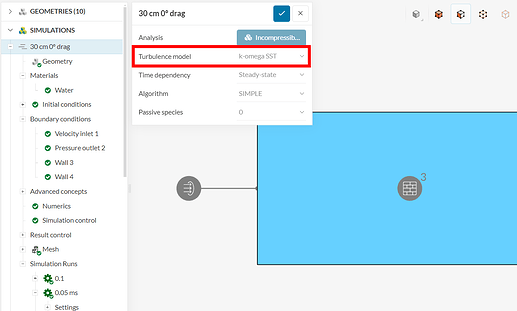
What I mean is that, when you chose the regime on the simulation tree, you have the option to chose either laminar or turbulent (as you did with your different simulations):
Once chosen, the regime will be applied to the simulation as a whole, no matter the calculated Re.
Even in regions where turbulence is minimal, this will make a difference since many things will be calculated if you apply turbulence. One of them, for example, is the increase in diffusion that turbulence models consider by adding a parameter \textcolor{red}{\mathrm{\mu_t}} in the Navier-Stokes equation:
\displaystyle \rho g - \frac{\partial \bar{p}}{\partial x_i} + \frac{\partial}{\partial x_j} \left [ (\mu + \textcolor{red}{\mathrm{\mu_t}}) \left ( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) \right] = \rho \left ( \frac{\partial \bar{u}_i}{\partial t} + \frac{\partial \bar{u}_j\bar{u}_i}{\partial x_j} \right)
Which, even if low in certain parts of the flow, will many times be large in comparison with the fluid’s viscosity (\mu)
I hope that helps 
Best,
Igor