Hi @ggiraldof and the rest of the staff involved in this issue,
I have been researching a little bit about my case that can be found here and some information regarding itself can be found in this other topic.
I have represented the absolute value of the dot products of the principal vectors in paraview so as to find the points where orthogonality is not reached. Representation is by means of spherical 3D Glyphs , scaled by module, so the bigger (and redder) the spheres are the further we are from orthogonality. Below some screenshots are presented.
v1·v2
v2·v3
v3·v1
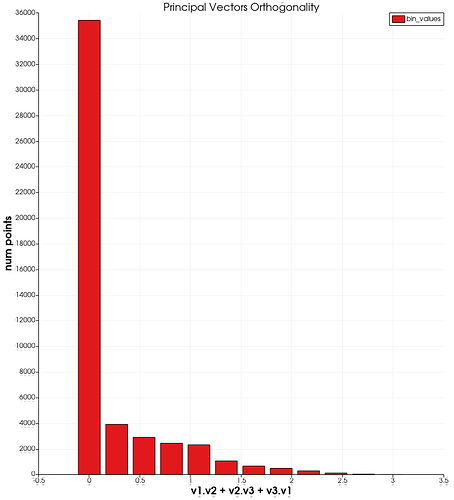
Furthermore, I summed all the results and got surprised to see that some points had a value close to 3, which means that all 3 principal vectors are close to be parallel. Something completelly unexpected…
v1·v2+v2·v3+v3·v1
I also investigated the histograms of the dot product values since in the previous images only the boundary values were represented. Only the histogram for v1·v2 is shown since the other two look very similar.
Historgram of v1·v2
Histrogram with the sum of dot products
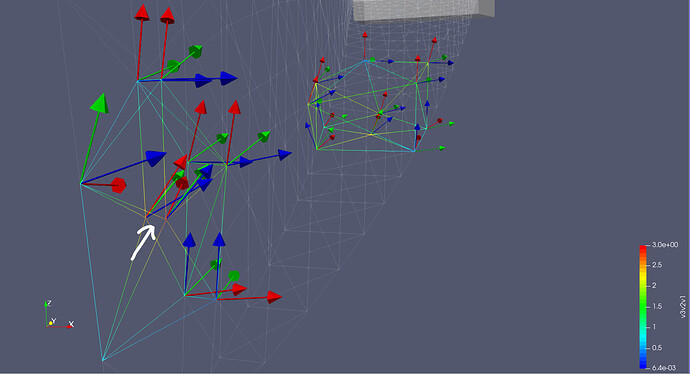
Finally, as a crosscheck, I extracted the tetrahedrons containing values greater that 2.25 of the sum of the 3 dot products and represented the principal vectors as glyphs. Tets are colored with the sum of the dot products so as to ease the search for the most critical points.
Below a couple of critical points (orange to red values) are highlighted to demonstrate that the 3 principal vectors are far from being orthogonal.
I hope that the information shared here can be helpful to illustrate the problem and to find a solution to it. If I can do something to help, just let me know.
Best,
Alex