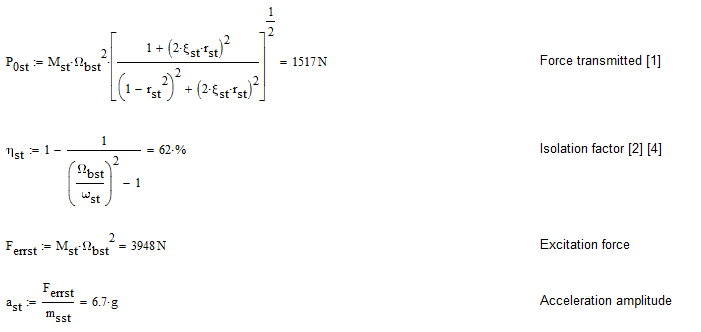Hi @jhorv_th @BenLewis!
First, thanks Ben for the great help and explanation!
Regarding the problem with the MUMPS solver, I guess a quick excursus would be helpful:
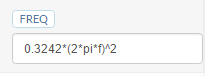
The MUMPS solver provides methods to estimate the quality of the solution of the linear system. On SimScale it can be controlled with the parameter Linear system relative residual of the MUMPs solver.
When doing error analysis for the solution of a linear system
$$ Ku = f $$
the main interest is the relative forward error {||\delta{u}||} \over {||u||}. It is the relative difference of the computed solution u^* from the actual (unknown) solution u. In most cases this error is unknown, but it can be estimated with an inverse approach using the backward error and the condition number of the solution matrix.
The backward error \eta(K,f) measures which modification \delta{f} to the RHS f would be needed to actually have u^* as the exact solution:
$$Ku^* = f + \delta{f}$$
The backward error is mainly introduced by rounding errors and should ideally be in the order of the machine precision (1e^{-15}).
The condition number indicates how sensitive the solution is to changes in the input variables, e.g. how much input errors influence output errors. For high condition numbers (\kappa(K)>1e^{10}), even small variations in the input can lead to drastic changes in the solution.
Putting both together we can state:
$$ {{||\delta{u}||} \over {||u||}} < C* \eta(K,f)* \kappa(K) $$
with C being some constant, thus the right hand side being an upper bound for the forward error.
Now if the product \eta(K,f)* \kappa(K) becomes larger than the user defined Linear system relative residual, the solver stops and ends with a message that the desired residual of the MUMPS solver could not be reached.
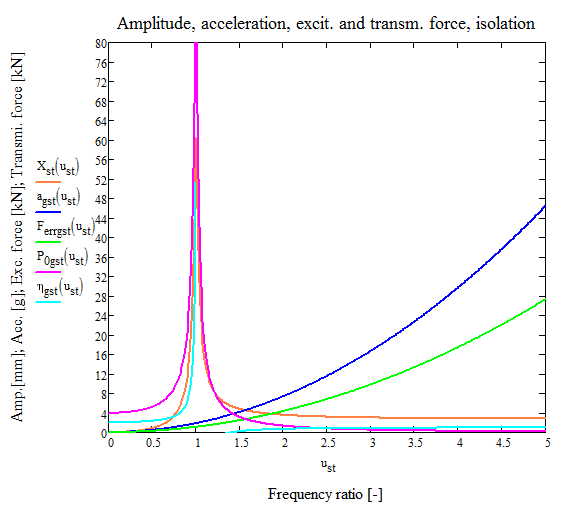
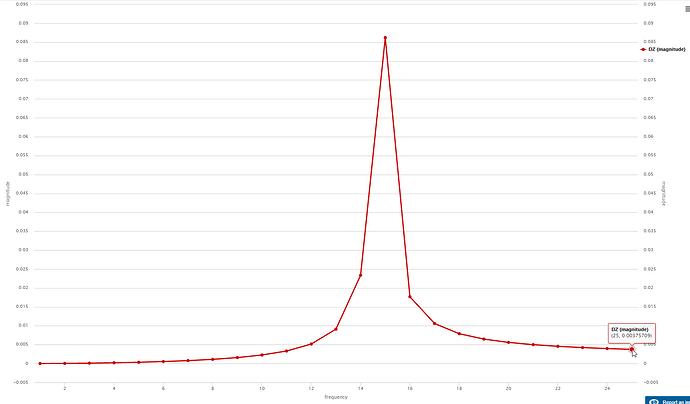
In this case here, we know that the error appears only below a certain frequency. As the matrix stays the same, we know that the reason must be an increasing backwards error for smaller frequencies, which is a common phenomena as the overall forces get lower, rounding errors get more important.
Now regarding the solution of this problem, there are several possibilities:
- increase the residual. A value of 1e-3 is not very uncommon and sometimes needed to be able to successfully run the analysis.
- turn off the relative residual check: using a negative value will deactivate the check. Since in this special case we already have a reference solution using MultFront we can be pretty confident to remove the test. (after I did it the solution time dropped from 100min with MultFront to 30min with MUMPS, giving the exact same results for the first 5 significant digits).
- change the settings of the MUMPS solver. Generally one could play with the selection of the renumbering tool, matrix type, in case of an Harmonic Analysis the possible choices are limited however
- improve the mesh quality. In this particular case I guess a big part of the problem is related to the bonded contact between the rubber and the frame where we have very high differences in mesh density on the master and slave side.
- check the coherence of your input data. Here, as already pointed out by @BenLewis, the stiffness of the rubber seems very low. In combination with the high Poissons ratio (0.499) and the very high stiffness of the other contact partner, steel, this will lead to a bad conditioning of the system matrix.
I hope this helps to understand the error reason and points to possible solutions.
Best,
Richard
![]()