Hi @pegacat,
I was wondering whether you managed to get the results you were looking for or not.
To help you out, here is some additional theory of what to expect for Re = 1e6. This was taken from free online MIT course lecture.
I will highlight some important things from page 73-74 below:
The first is as you already mentioned regarding the flow regime at Re=1e6. The thing to point out here is that you have a “Turbulent boundary layer” both upstream and uptill the separation point.
To model “boundary layer separation” accurately it is important NOT to use “wall functions” but to resolve the flow completely by setting the option to “set gradient to zero” in the wall boundary condition. For this Y+ of less than 1-1.5 must be ensured.
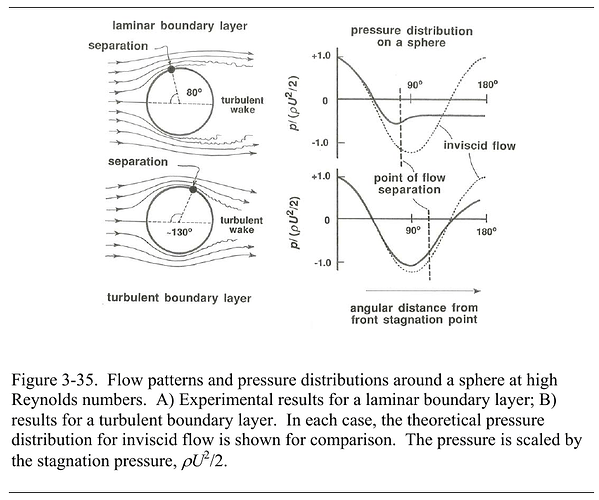
In this case separation takes place farther around toward the rear of the sphere, at a position about 120–130° from the front stagnation point. The wake becomes contracted compared to its size when the separation is laminar, and consequently the low pressure exerted on the surface of the sphere within the separation region acts over a smaller area. Also, the pressure itself in this region is not as low (Figure below).
Figure by MIT open course ware
.
So, try to do the following:
1- See if you get a similar normalised pressure profile on the cylinder as shown in figure above (the lower graph)
2- and check if you have flow separation behind the sphere by plotting the “wall shear stress” on the sphere.
Then you will be able to better decide which type of flow you are getting ( i.e low or high Re)
Also for Re = 1e6 you will get a lesser drag value than Re < 1e6. This is called “drag crisis”. Also mentioned in the document page 74.
As for the calculation of K and Omega in ‘Initial conditions’ use the values based on formulation given here " K-Omega formulation" . ( use second formula for Omega)
I Hope this helps.
Best,
Ali