Hi @jpola,
I have taken a brief look at your project and also done a number of sample runs to see what could be the issue.
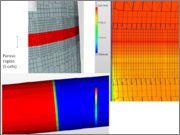
So, I have done 4 case studies of analysis type “Compressible , Turbulent (K-OmegaSST) , Steady State with Porous Media” with your geometry .
For these cases the following were kept exactly the same;
1- Mesh
2- Model
3- Initial Condition
4- Boundary Conditions
5- Numerics and simulation control
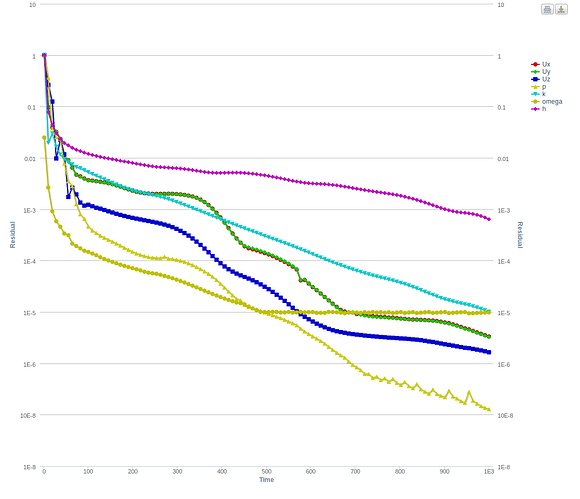
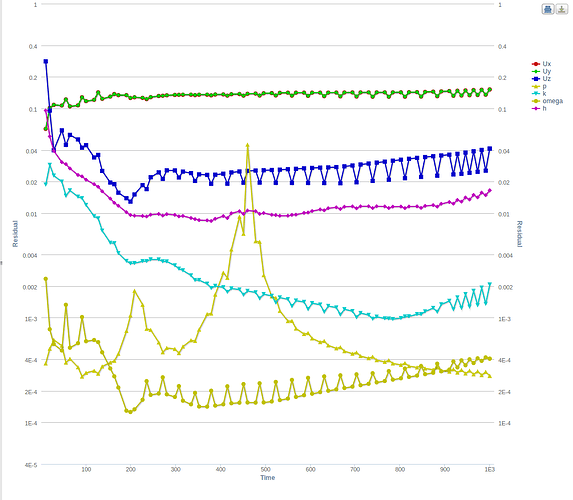
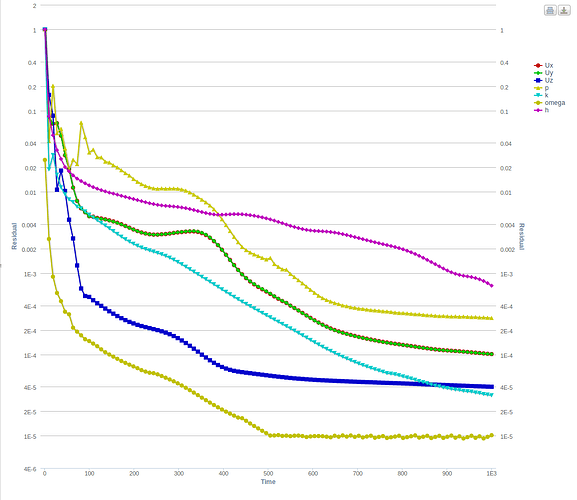
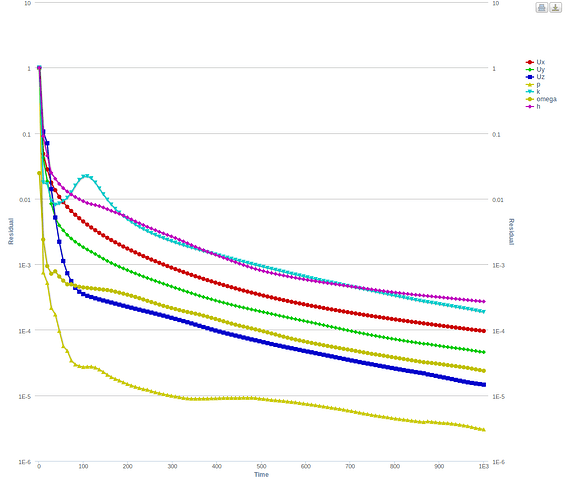
So the only thing different for the cases was the “Porous Media settings”. Below are the details and the convergence plots.
Case-1 : with the 'default values of Darcy-Forchheimer Coefficients ’
Case-2 : with the ’ Fixed Coefficients using your values’
Case-3 : with the ’ Fixed Coefficients, but using lower order values compared to your values’
Case-4 : with the ’ Fixed Coefficients, but using default values’
Firstly, based on these plots I see good convergence for Cases 1, 3 and 4 in comparison to your case. Especially when comparing case 2 and case 3, where the only difference is the order of the values.
Secondly, based on the results (not shown here for simplicity) I observe a pressure drop across the porous region for Cases 1, 3 and 4 , that should be expected. While, Case-2 there seems to give a pressure rise. Now I’m not sure if that is what you would expect but it could be a reason for the oscillating behaviour of the residuals.
If you do expect a ‘pressure rise’ for the selected coefficients ( and are sure about the values) then another reason for an oscillating residual behaviour could be a course mesh. Perhaps you could try with a fine mesh and still if you get an oscillating behaviour then it would perhaps mean that the flow is undergoing transient effects with these values of Porous media and can not reach a steady state, so no relative convergence exists for a steady state analysis. Thus you would require a Transient analysis to get to a more relative converged state.
Lastly, It is generally recommended to use low relaxation factors in the numerics for such a compressible case to avoid instabilities and divergence in the first few iterations. ( for these cases they were the same)
Thus, as can be observed from the cases, the Porous media Coefficients have a significant effect on the flow topology and in getting a converged result.
I will send you the link of the Project with these cases in a private message soon.
I hope these observations will be helpful for you and if I have missed something then please feel free to let me know.
Best,
Ali.