PIMPLE pressure residual

Using SimScale Fluid Flow / CFD
1

Hi, trying my first transient case I get a steady pressure residual of about 0.28, can´t see where the problem is.
Test case is a box with an inlet and outlet pipe, starts flowing from standstill during 2 seconds.

These are the main parameters for Sim control and numerics. Are there described anywhere? I tweaked them without success to warranty a relative improvement per “inner loop” and a absolute tolerance for the final iteration per timestep (if I undestood well…).

Relaxation factor for field p 0.3
Relaxation factor for equation U 0.7
Number of outer correctors 5 ← not clear what does it mean
Number of correctors 5 ← what is this? iterations at same timestep?
Number of non-orthogonal correctors 1
Pressure reference cell 0
Pressure reference value 0
Correct the flux No
Relaxation factor for field k 0.7
Relaxation factor for field omega 0.7
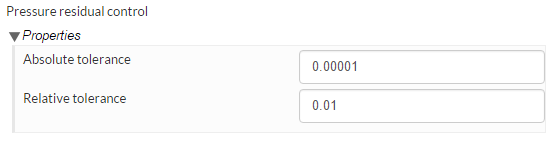
Pressure solver- abs. tolerance 0 rel. tolerance 0.05
Pressure final solver- abs. tolerance 1e-7 rel. tolerance 0
…

Solver Log:

…
ExecutionTime = 3549.78 s ClockTime = 3573 sCourant Number mean: 0.0588417325689 max: 0.698605123499deltaT = 0.00254223447539Time = 1.93135966916PIMPLE: iteration 1DILUPBiCG: Solving for Ux, Initial residual = 0.00067717050359, Final residual = 7.01630659014e-06, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 0.000676680997124, Final residual = 3.25648739925e-06, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 0.000220470270686, Final residual = 1.04770824031e-06, No Iterations 1DICPCG: Solving for p, Initial residual = 0.26083862015, Final residual = 0.0128328088187, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0201247601123, Final residual = 0.000988426342042, No Iterations 88time step continuity errors : sum local = 2.58509095723e-07, global = -9.84574629e-09, cumulative = -0.000142228323046DICPCG: Solving for p, Initial residual = 0.172548296439, Final residual = 0.00837958242649, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0139416036058, Final residual = 0.000671363205226, No Iterations 89time step continuity errors : sum local = 1.75797767922e-07, global = -1.35255889533e-08, cumulative = -0.000142241848635DICPCG: Solving for p, Initial residual = 0.172482402517, Final residual = 0.00838655106847, No Iterations 7DICPCG: Solving for p, Initial residual = 0.013957980873, Final residual = 0.000669614290432, No Iterations 89time step continuity errors : sum local = 1.75354402065e-07, global = -1.34404299931e-08, cumulative = -0.000142255289065DICPCG: Solving for p, Initial residual = 0.172476812052, Final residual = 0.00839103262979, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0139619675664, Final residual = 0.000676224318838, No Iterations 89time step continuity errors : sum local = 1.77092126734e-07, global = -1.33635544277e-08, cumulative = -0.000142268652619DICPCG: Solving for p, Initial residual = 0.172475121174, Final residual = 0.00838889948961, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0139599759824, Final residual = 0.000671208374209, No Iterations 89time step continuity errors : sum local = 1.75780361693e-07, global = -1.33847841885e-08, cumulative = -0.000142282037403PIMPLE: iteration 2DILUPBiCG: Solving for Ux, Initial residual = 0.000230862225256, Final residual = 9.24944728141e-07, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 0.000229791642062, Final residual = 1.12927007786e-06, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 7.46074665625e-05, Final residual = 4.70547766495e-06, No Iterations 1DICPCG: Solving for p, Initial residual = 0.168053905339, Final residual = 0.00833821031354, No Iterations 6DICPCG: Solving for p, Initial residual = 0.0127389031591, Final residual = 0.000612620555314, No Iterations 90time step continuity errors : sum local = 1.59164242814e-07, global = -1.45580404022e-08, cumulative = -0.000142296595444DICPCG: Solving for p, Initial residual = 0.112859824716, Final residual = 0.00554343227284, No Iterations 6DICPCG: Solving for p, Initial residual = 0.00884516237995, Final residual = 0.000409448243523, No Iterations 93time step continuity errors : sum local = 1.06492229647e-07, global = -1.86208698096e-08, cumulative = -0.000142315216314DICPCG: Solving for p, Initial residual = 0.112801049958, Final residual = 0.00554351299791, No Iterations 6DICPCG: Solving for p, Initial residual = 0.00884869281756, Final residual = 0.00040605302623, No Iterations 93time step continuity errors : sum local = 1.05624963726e-07, global = -1.84621719217e-08, cumulative = -0.000142333678485DICPCG: Solving for p, Initial residual = 0.112795414624, Final residual = 0.00554726589471, No Iterations 6DICPCG: Solving for p, Initial residual = 0.00885202620444, Final residual = 0.000441219158184, No Iterations 92time step continuity errors : sum local = 1.14778891329e-07, global = -1.75628374635e-08, cumulative = -0.000142351241323DICPCG: Solving for p, Initial residual = 0.112797570301, Final residual = 0.0055496029817, No Iterations 6DICPCG: Solving for p, Initial residual = 0.00885423573902, Final residual = 0.000439548973407, No Iterations 92time step continuity errors : sum local = 1.14345769855e-07, global = -1.75404251375e-08, cumulative = -0.000142368781748PIMPLE: iteration 3DILUPBiCG: Solving for Ux, Initial residual = 9.74337511592e-05, Final residual = 1.01633014915e-06, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 9.66201322149e-05, Final residual = 8.98606260137e-07, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 3.03794753981e-05, Final residual = 2.34876768988e-07, No Iterations 1DICPCG: Solving for p, Initial residual = 0.109610294541, Final residual = 0.00547950776607, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00780181232291, Final residual = 0.000385452749946, No Iterations 96time step continuity errors : sum local = 9.95931685658e-08, global = -2.1167702001e-08, cumulative = -0.00014238994945DICPCG: Solving for p, Initial residual = 0.0745798976194, Final residual = 0.00369385136774, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00542485409894, Final residual = 0.000248124902362, No Iterations 177time step continuity errors : sum local = 6.41672031837e-08, global = -1.09069525043e-11, cumulative = -0.000142389960357DICPCG: Solving for p, Initial residual = 0.0737924707288, Final residual = 0.00365076436865, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00537055310656, Final residual = 0.000261809472139, No Iterations 96time step continuity errors : sum local = 6.83764321441e-08, global = -1.44243698484e-08, cumulative = -0.000142404384727DICPCG: Solving for p, Initial residual = 0.0743198540053, Final residual = 0.00368518421105, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00541356467056, Final residual = 0.000268882190937, No Iterations 176time step continuity errors : sum local = 6.97400703743e-08, global = 1.9327140544e-10, cumulative = -0.000142404191455DICPCG: Solving for p, Initial residual = 0.073797419797, Final residual = 0.00365329043978, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00537280661118, Final residual = 0.000262636869524, No Iterations 96time step continuity errors : sum local = 6.8585743172e-08, global = -1.44772393998e-08, cumulative = -0.000142418668695PIMPLE: iteration 4DILUPBiCG: Solving for Ux, Initial residual = 5.11468792423e-05, Final residual = 6.22052903696e-07, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 5.06606415917e-05, Final residual = 5.51056299633e-07, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 1.49111345734e-05, Final residual = 1.13289978527e-07, No Iterations 1DICPCG: Solving for p, Initial residual = 0.0720743455083, Final residual = 0.00307886521672, No Iterations 5DICPCG: Solving for p, Initial residual = 0.0047398410707, Final residual = 0.000235625125893, No Iterations 176time step continuity errors : sum local = 6.07818929628e-08, global = 5.9772860428e-12, cumulative = -0.000142418662718DICPCG: Solving for p, Initial residual = 0.0490839043748, Final residual = 0.0020781884575, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00326977259385, Final residual = 0.000161434113085, No Iterations 177time step continuity errors : sum local = 4.20399036266e-08, global = -4.69035020053e-10, cumulative = -0.000142419131753DICPCG: Solving for p, Initial residual = 0.049066497006, Final residual = 0.0020796949329, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00327303467306, Final residual = 0.000163417741286, No Iterations 179time step continuity errors : sum local = 4.25487254363e-08, global = -9.20300141137e-10, cumulative = -0.000142420052053DICPCG: Solving for p, Initial residual = 0.0490689722987, Final residual = 0.0020809380721, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00327376295612, Final residual = 0.000162704803703, No Iterations 203time step continuity errors : sum local = 4.23604701259e-08, global = -3.10427176063e-10, cumulative = -0.00014242036248DICPCG: Solving for p, Initial residual = 0.0490675631085, Final residual = 0.00208068299735, No Iterations 5DICPCG: Solving for p, Initial residual = 0.00327352655394, Final residual = 0.000156857625855, No Iterations 177time step continuity errors : sum local = 4.0840931101e-08, global = -4.3685499717e-10, cumulative = -0.000142420799335PIMPLE: iteration 5DILUPBiCG: Solving for Ux, Initial residual = 4.36351074985e-05, Final residual = 1.05810947501e-06, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 4.31542944718e-05, Final residual = 9.39886200428e-07, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 1.27041371012e-05, Final residual = 1.7212989725e-07, No Iterations 1DICPCG: Solving for p, Initial residual = 0.19925535684, Final residual = 0.00921167495846, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0211370181632, Final residual = 0.00102437583511, No Iterations 88time step continuity errors : sum local = 2.54313768143e-07, global = 2.64775747689e-09, cumulative = -0.000142418151577DICPCG: Solving for p, Initial residual = 0.00809156400505, Final residual = 0.00039534549904, No Iterations 23DICPCG: Solving for p, Initial residual = 0.00107205603933, Final residual = 5.2255932566e-05, No Iterations 191time step continuity errors : sum local = 1.28666768962e-08, global = 1.79296652813e-10, cumulative = -0.000142417972281DICPCG: Solving for p, Initial residual = 0.000817880278234, Final residual = 3.96852712979e-05, No Iterations 30DICPCG: Solving for p, Initial residual = 9.52355546567e-05, Final residual = 4.45140291837e-06, No Iterations 195time step continuity errors : sum local = 1.07174128772e-09, global = 2.04157778904e-12, cumulative = -0.000142417970239DICPCG: Solving for p, Initial residual = 9.51422305492e-05, Final residual = 4.55776409886e-06, No Iterations 7DICPCG: Solving for p, Initial residual = 7.39377842642e-06, Final residual = 3.58555413841e-07, No Iterations 206time step continuity errors : sum local = 8.65552468387e-11, global = 1.06930941732e-12, cumulative = -0.00014241796917DICPCG: Solving for p, Initial residual = 1.01329765754e-05, Final residual = 4.76359018717e-07, No Iterations 6DICPCG: Solving for p, Initial residual = 8.42889196851e-07, Final residual = 9.70790719976e-08, No Iterations 25time step continuity errors : sum local = 2.34383458815e-11, global = 1.30917727482e-12, cumulative = -0.000142417967861DILUPBiCG: Solving for omega, Initial residual = 0.000104256674898, Final residual = 8.77058854145e-07, No Iterations 1DILUPBiCG: Solving for k, Initial residual = 0.00118348516952, Final residual = 3.65467230944e-06, No Iterations 2ExecutionTime = 3554.29 s ClockTime = 3578 sregIOobject::readIfModified() : Re-reading object controlDict from file "system/controlDict"Courant Number mean: 0.0588593412964 max: 0.698644190216deltaT = 0.00254223447539Time = 1.93390190364PIMPLE: iteration 1DILUPBiCG: Solving for Ux, Initial residual = 0.000676439757255, Final residual = 6.98632492088e-06, No Iterations 1DILUPBiCG: Solving for Uy, Initial residual = 0.000676091899832, Final residual = 3.22835339646e-06, No Iterations 1DILUPBiCG: Solving for Uz, Initial residual = 0.000220311649741, Final residual = 1.04791680268e-06, No Iterations 1DICPCG: Solving for p, Initial residual = 0.260841984527, Final residual = 0.0128160384365, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0201097630522, Final residual = 0.000993748678274, No Iterations 88time step continuity errors : sum local = 2.60020830834e-07, global = -9.81709555841e-09, cumulative = -0.000142427784956DICPCG: Solving for p, Initial residual = 0.172548480378, Final residual = 0.00836800226039, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0139308396223, Final residual = 0.000672381120172, No Iterations 89time step continuity errors : sum local = 1.76144842506e-07, global = -1.35198357765e-08, cumulative = -0.000142441304792DICPCG: Solving for p, Initial residual = 0.172483279818, Final residual = 0.00837454814298, No Iterations 7DICPCG: Solving for p, Initial residual = 0.0139468168216, Final residual = 0.000672319201463, No Iterations 89time step continuity errors : sum local = 1.76143223259e-07, global = -1.34247636262e-08, cumulative = -0.000142454729556DICPCG: Solving for p, Initial residual = 0.172477246545, Final residual = 0.00837925716192, No Iterations 7DICPCG: Solving for p, Initial residual = 0.013950990446, Final residual = 0.000676260951986, No Iterations 89time step continuity errors : sum local = 1.77182708986e-07, global = -1.33631245007e-08, cumulative = -0.00014246809268DICPCG: Solving for p, Initial residual = 0.17247576963, Final residual = 0.00837813273622, No Iterations 7DICPCG: Solving for p, Initial residual = 0.013949877448, Final residual = 0.000671973441343, No Iterations 89time step continuity errors : sum local = 1.7606135292e-07, global = -1.33757366164e-08, cumulative = -0.000142481468417PIMPLE: iteration 2DILUPBiCG: Solving for Ux, Initial residual = 0.000230631575234, Final residual = 9.17008043666e-07, No Iterations 1

2

Project link

3

Hello!

This is expected to happen. All comes down to the difference of the way solution is obtained for steady state simulations and for transient ones.

With steady state we remove the time dependency from all the equations and “time” becomes a “step towards the solution”. In fact each step is another approximation of the solution, based on the results of the previous one.
The continuity and momentum equations will not necessarily match, and only when all the residuals go sufficiently low can we say that the results are close to reality.
For this reason it is not important what is the time step length- they just represent the number in the sequence of approximations. I usually set dt=1 for steady state to have it easier to track which iteration are we at.

All becomes different with transient simulations. Here we have to ensure convergence of the solution at each and every step on the way. All equations: mass, momentum, temperature, etc need to converge for the time spot at which we are. This means that the residuals need to reach a small, pre-defined value for each and every time step. If your residual got “stuck” at a certain value, this means that the solution reached the sufficient accuracy for this step, and that it is around the mentioned value. In fact it is expected to have the residual plots to look like the one you presented for steady state simulation.
There are 2 ways that the residuals are controlled.

  • First one is the absolute value of the residual. As soon as it goes below it, the calculation for the particular time step is assumed converged.
  • The second one is the relative change of residual. If the residual improvement between two consecutive sub-iterations
    is lower than this value, again we assume convergence within the step.
    Most likely your simulation gets the second criterion matched and stops further approximations within the time steps.

If you are not satisfied with the residual levels (of fear that the results will involve too much numerical errors), you can sharpen the criteria. You can do that in Numerical settings, under Details for the solver of the field you are interested in (see example screenshot).

Most transient simulations might have some trouble in the few first iterations, since you give them a big “shock”- imagine, you have a still environment and then BAM: 2m/s blower enters the system. That is a hard thing to converge. For this reason it might be useful to use a slow initialization of the flow. Give it a function value or upload the table that will ramp the inlets during first one or two seconds and later keep them at constant levels. It will definitely improve the convergence.

In the end, I think your simulation looks quite good. Just decide if it makes sense or not.

Hope this post helps :wink: Keep the flow running!

4

Thanks for the analysis Pawel.

I understand that the solver makes some time steps and for each timestep does some “inner” interations to improve the per-timestep solution (PIMPLE iterations in the log). How many are sensible to use for these?

My guess is that i.e. “pressure solver” in “numerics” means the solver parameters used for the inner “PIMPLE” interations. And “pressure final solver” are the parameters used for the final solution for each timestep. Please clarify if that is correct.

Additionally, examining the log for an example time step i see:

PIMPLE iteration 5 per Time = 1.98306656483
(… can be seen very low residuals for u, k, e solvers, assume they are ok…)
GAMG: Solving for p, Initial residual = 0.224802869411, Final residual = 0.00194559561335, No Iterations 5 <----- seems ok, reduces quite a lot from initial 0.22 residual

Then appears what I interpret as the “final solution” for Timestep=1.98306656483
time step continuity errors : sum local = 1.41352956398e-11,
global = -1.09267375332e-13, cumulative = -2.18735316637e-06
<–seems quite low, doesn´t it?
DICPCG: Solving for p, Initial residual = 0.0197956354699, Final residual = 9.84861526621e-08, No Iterations 289
*<–is this the final pressure for this time step, residual is order of E-08, why in the convergence plots is seen >0.2?

Thanks

ourant Number mean: 0.0435218200237 max: 0.495394120561
deltaT = 0.00188149279701
Time = 1.98306656483
PIMPLE: iteration 1
DILUPBiCG: Solving for Ux, Initial residual = 0.00050052459909, Final residual = 3.37052297586e-06, No Iterations 1
DILUPBiCG: Solving for Uy, Initial residual = 0.000500141451536, Final residual = 3.73522104179e-06, No Iterations 1
DILUPBiCG: Solving for Uz, Initial residual = 0.000152610386058, Final residual = 6.09070683502e-07, No Iterations 1
GAMG: Solving for p, Initial residual = 0.293951562137, Final residual = 0.00272245867537, No Iterations 5
time step continuity errors : sum local = 3.58424756523e-07, global = 5.1312783749e-11, cumulative = -2.1873070691e-06
GAMG: Solving for p, Initial residual = 0.192535270872, Final residual = 0.00188873795013, No Iterations 5
time step continuity errors : sum local = 2.67144576427e-07, global = 1.90763760762e-11, cumulative = -2.18728799273e-06
…
PIMPLE: iteration 4
DILUPBiCG: Solving for Ux, Initial residual = 4.36557511997e-05, Final residual = 9.02384302342e-07, No Iterations 1
DILUPBiCG: Solving for Uy, Initial residual = 4.33365051141e-05, Final residual = 3.76235817734e-07, No Iterations 1
DILUPBiCG: Solving for Uz, Initial residual = 1.22374476706e-05, Final residual = 4.31720650212e-08, No Iterations 1
GAMG: Solving for p, Initial residual = 0.0799354473485, Final residual = 0.000792757801832, No Iterations 5
time step continuity errors : sum local = 1.21887866078e-07, global = 8.51433625418e-12, cumulative = -2.18724943566e-06
GAMG: Solving for p, Initial residual = 0.0549521326505, Final residual = 0.000388693847237, No Iterations 6
time step continuity errors : sum local = 6.1249609414e-08, global = -1.22148647794e-11, cumulative = -2.18726165053e-06
PIMPLE: iteration 5
DILUPBiCG: Solving for Ux, Initial residual = 3.83524828097e-05, Final residual = 8.52483020673e-07, No Iterations 1
DILUPBiCG: Solving for Uy, Initial residual = 3.80790931965e-05, Final residual = 2.77012552423e-07, No Iterations 1
DILUPBiCG: Solving for Uz, Initial residual = 1.04970899256e-05, Final residual = 6.23538043877e-08, No Iterations 1
GAMG: Solving for p, Initial residual = 0.224802869411, Final residual = 0.00194559561335, No Iterations 5
time step continuity errors : sum local = 3.51472310813e-07, global = -9.1406575625e-11, cumulative = -2.1873530571e-06
DICPCG: Solving for p, Initial residual = 0.0197956354699, Final residual = 9.84861526621e-08, No Iterations 289
time step continuity errors : sum local = 1.41352956398e-11, global = -1.09267375332e-13, cumulative = -2.18735316637e-06
DILUPBiCG: Solving for epsilon, Initial residual = 0.000195925107015, Final residual = 1.32896679185e-06, No Iterations 1
DILUPBiCG: Solving for k, Initial residual = 0.000534721488859, Final residual = 5.44053673294e-06, No Iterations 1
ExecutionTime = 854.66 s ClockTime = 875 s

5

Greetings!

Indeed, the PIMPLE solver uses these iterations to obtain coupling between continuity and momentum equations.

Usually 2-3 is enough. 4 can be tried if you want to have a problem of accumulation of residual error. More than that will not significantly improve the results.

That is correct. If we have 3 inner-iterations, we will have 2 first done with “general” settings, and the last one will be done with the “final” params.

The most important is the last available residual for each of the fields. Those residuals should be as small as possible. In fact, even the one for pressure is

DICPCG: Solving for p, Initial residual = 0.0197956354699, Final residual = 9.84861526621e-08, No Iterations 289

This means that the solver converges. The second important check is the continuity equation and its behavior over time. In your case you get a reasonable behavior with low continuity errors.

time step continuity errors : sum local = 1.41352956398e-11, global = -1.09267375332e-13, cumulative = -2.18735316637e-06

Anytime the continuity error would rise more that 1%o of the simulation flow, I would start feeling uncomfortable about the results.

Again, hope this brought some lite to the subject.
All the best!

6

Dear Pawel,

So I understand it is working correctly; then, what sense has the pressure residual showing as 0.25 in the convergence plot?
The final PIMPLE residual per Time = 1.98306656483 is DICPCG: Solving for p, Initial residual = 0.0197956354699, Final residual = 9.84861526621e-08,

At least for the pressure the solver log just doesn´t match to the convergence plot. I think I want to see the final residual per timestep, why the initial or other residual should matter to me?

BTW, I found this illustrative reference, to see how the algorithm is working it is quite clear showing the convergence plot vs iterations (instead of vs time):
https://openfoamwiki.net/index.php/OpenFOAM_guide/The_PIMPLE_algorithm_in_OpenFOAM

Would be sensible to use a default parameters Outer-inner iterations higher?.
i.e. from your comment (no sure if changed loops)
(Pimple loops) nouterCorrectors : ¿5? depends on relax factors
(pressure correction loops)nCorrectors: ¿3?

Regards

7

Hello!

Got stranded with the meetings… I need to get the forum as a starting page.

The residual plots that you are seeing on the platform demonstrate the “initial” residual. It is the very first one you get for each field at any time step.
For this reason they do not change (much) during transient simulations. Each time advancement will create an imbalance in the equations which needs to be converged. Your example describes it very well. What you see is always the pick of the convergence “teeth”.

Regarding the iteration coefficients, it is quite problem dependent. I strongly encourage you to play around and see what works best for you.

Best,
Pawel

8

Hi,
so as far as I see it, the convergence plot, as it is now, shows misleading information.

I want to know that the simulation is progressing correctly, the info of initial residual of P for each timestep is of doubtfull utility. In my case as it starts about 0.2, I thought that the final solution had a very high pressure residual, so was not usable at all.

Please consider to modify that plot, or even plot vs iterations, instead of vs time, to check that final residual per timestep progress to a low enough value. Seeing only the initial is just not sensible.

Regards

9

Thank you @rarrese and @psosnowski for your remarks. Let’s see if we can bring this to a conclusion.

Firstly, residual monitoring: initial residual is calculated from the field before solving for it, whereas final residual is computed after. In a healthy case, both initial and final residuals decrease in the course of the simulation. However, achieving a small value for one does not guarantee convergence of the other. That said, the initial residual is still more important when convergence of the simulation as a whole is being monitored. Plotting final residual does not contribute much to that.

Secondly, the apparent inconsistency between the log and the convergence plot. With the above statement in mind, let’s have a look at log for Time = 1.98306656483 that you mentioned. The residual value for pressure from the plot reads ca. 0.2939, which is the same as pressure’s initial residual for the first GAMG solving of the first PIMPLE iteration:
Time = 1.98306656483 PIMPLE: iteration 1 DILUPBiCG: Solving for Ux, Initial residual = 0.00050052459909, Final residual = 3.37052297586e-06, No Iterations 1 DILUPBiCG: Solving for Uy, Initial residual = 0.000500141451536, Final residual = 3.73522104179e-06, No Iterations 1 DILUPBiCG: Solving for Uz, Initial residual = 0.000152610386058, Final residual = 6.09070683502e-07, No Iterations 1 GAMG: Solving for p, Initial residual = 0.293951562137, Final residual = 0.00272245867537, No Iterations 5 time step continuity errors : sum local = 3.58424756523e-07, global = 5.1312783749e-11, cumulative = -2.1873070691e-06 GAMG: Solving for p, Initial residual = 0.192535270872, Final residual = 0.00188873795013, No Iterations 5 time step continuity errors : sum local = 2.67144576427e-07, global = 1.90763760762e-11, cumulative = -2.18728799273e-06

I hope this helps. Let me know if you would like to discuss this further.
Babak

10

Hi,

So as initial residual is very high and remains steady,
should I understand that the problem is that the setup of the problem has some issue?
What puzzles me now is: initial residuals seems to stabilize but to a high value for pressre, final residual however seems to get low, but maybe not so much (1E-3), so… can I trust the results or not?

11

The role of residuals in determining if simulation results are to be trusted should not be misunderstood. Reaching steady residuals means that the solution has converged to a value. Whether this value is correct or not can ultimately be concluded by monitoring the solution field.

There are a number of factors that could cause large pressure residuals. You could perform a convergence study to determine if results are reliable. In case of this simulation, consider the following:

  • Mesh quality could impose a lower limit on residual values. Even though your mesh looks good, convergence of the solution by refining the mesh should be studied. Specifically consider boundary vicinity and regions of high gradient.
  • Linear solvers have an impact on convergence behavior. You could try a different solver for pressure to see if residuals change.
  • Absolute and relative residuals must be considered carefully. We have had a discussion on this here. As demonstrated, residuals must be chosen in accordance with all variables. In your case, relative pressure residual could be reconsidered.

This list is in fact longer. You could reconsider the choice of the turbulence model, turbulence wall treatment, numerical schemes, etc. However, be aware that the residual value in itself is not the issue, e.g. one could under-relax to get smaller residuals, but this does not improve the solution. Whatever you do, convergence of the solution field is the deciding factor.

1 Like
12

Hi @gholami

From the solver log., final PIMPLE iteration info for each time step:

Time = 1.98306656483
DICPCG: Solving for p, Initial residual = 0.0197991548329, Final residual = 9.06271128355e-08
Time = 1.98494805762
DICPCG: Solving for p, Initial residual = 0.0197956354699, Final residual = 9.84861526621e-08
Time = 1.98682955042
DICPCG: Solving for p, Initial residual = 0.0197905132652, Final residual = 9.2114101519e-08
Time = 1.98871104322
DICPCG: Solving for p, Initial residual = 0.0197870888574, Final residual = 9.76194018977e-08
Time = 1.99059253601
DICPCG: Solving for p, Initial residual = 0.0197816980887, Final residual = 9.5613143425e-08
Time = 1.99247402881
DICPCG: Solving for p, Initial residual = 0.0197737702382, Final residual = 9.41448290391e-08
Time = 1.99435552161
DICPCG: Solving for p, Initial residual = 0.0197786054918, Final residual = 9.37699334508e-08
Time = 1.99623701441
DICPCG: Solving for p, Initial residual = 0.0197702410006, Final residual = 9.50475283695e-08
Time = 1.9981185072
DICPCG: Solving for p, Initial residual = 0.0197648008975, Final residual = 9.49425473474e-08,
Time = 2
DICPCG: Solving for p, Initial residual = 0.0197609122142, Final residual = 9.43076010072e-08,

The final pressure residual is stabilized and really low due to a tight “final solver” convergence tolerance. Continuity error is also low.

I don´t know why the initial residual always starts relatively high even after 4 previous PIMPLE loops, it might be a side effect of some “not good” numerics parameters, but as far as final field results, these are quite “converged and low” and I must insist on that the info I do see on the convergence plot is not showing that in any sense.

As suggested, I tried to change the inner tolerance to absolute 1e-3 and 1e-5and but solver plot initial residuals behaviour is almost the same (with same mesh).

I tried with a “auto-fine” mesh and it seems to improve very slightly (from 0.20 to 0.16 or so) the “converged” initial residual of first iteration per timestep, but I can´t see the.motivation to use that fine mesh if the final residual of the PIMPLE loop per each timestep is in any case very low (and flow patter quite similar).

My impression si that an additional plot showing (iteration vs residual) or (time vs final residual of the imple loop) would be much clearer of how the progress of the PIMPLE calculation is working.

Regards

13

Hi

I might be able to help.

Lets start with the basics. In a steady state SIMPLE loop, velocities and pressures are reduced every iteration until all parameters reached values small enough for convergence. The reduction of these values per iteration may or may not be a very smaller number. As long as the overall reduction meets convergence requirement, the simulation is over.

Now, in a time dependent SIMPLE loop, all the parameters ( velocities and pressure etc ) are required to reduce to values small enough for convergence in each time step. It is easier to view transient SIMPLE as a lot of steady state SIMPLE loops over multiple time steps. Now because within each time step, there are multiple steady state SIMPLE loops, we call it ‘iterative time advancement’.

Lets move onto PISO. The difference between PISO and SIMPLE in terms of time advancement is that PISO doesnt require an iterative process, and is therefore called non-iterative time advancement. Here by iterative I mean multiple PISO loops each time step ( just like transient SIMPLE ). However, for a solution to converge when solving with PISO, you would then need to do iterations within the PISO loop itself. Note that there is a difference between iterations within each PISO loop, and in between PISO loops. For PISO to yield promising results, it is generally required to go through two pressure corrector loops ( each of these two loops will then go through multiple iterations to reduce residuals ) and one loop for each velocity component with multiple iterations.

The PIMPLE algorithm is a combination of PISO and SIMPLE, and is very similar to transient SIMPLE with PISO replacing steady state SIMPLE. The PISO loops are repeated until the convergence requirement is reached.

In short, transient SIMPLE is a lot of steady state SIMPLE loops per time step; PIMPLE is a lot of PISO loops per time step. For transient SIMPLE, solutions converge when the initial residuals at the start of each steady state SIMPLE loop fall below pre-defined values; for PIMPLE to converge, the initial residuals at the start of each PISO loop will fall below pre-defined values.

5 Likes
14

To give you an example:

solvers
{
    p
    {
        solver          GAMG;
        tolerance       1e-05;
        relTol          0;
        smoother        GaussSeidel;
        cacheAgglomeration true;
        nCellsInCoarsestLevel 10;
        agglomerator    faceAreaPair;
        mergeLevels     1;
    }

   pFinal
    {
        solver          GAMG;
        tolerance       1e-06;
        relTol          0;
        smoother        GaussSeidel;
        cacheAgglomeration true;
        nCellsInCoarsestLevel 10;
        agglomerator    faceAreaPair;
        mergeLevels     1;
    }

   "(U|k|epsilon)"
    {
        solver          smoothSolver;
        smoother        symGaussSeidel;
        tolerance       1e-05;
        relTol          0;
    }

   "(U|k|epsilon)Final"
    {
        solver          smoothSolver;
        smoother        symGaussSeidel;
        tolerance       1e-05;
        relTol          0;
    }
}

PIMPLE
{
    nOuterCorrectors 20;
    nCorrectors     2;
    nNonOrthogonalCorrectors 0;
    residualControl
    {
        "(U|k|epsilon)"
        {
                tolerance  1e-3;
                relTol      0;
        }
        p
        {
                tolerance  1e-3;
                relTol      0;
        }
     }
}

relaxationFactors
{
	fields
    {
    	p                         0.3;
    }
    equations
    {
        "(U|k|epsilon)"           0.9;
        "(U|K|epsilon)Final"      1;
    }
}

The tolerances 1e-05 and 1e-06 are for each PISO loop. When the final residuals within each PISO loop fall below these values, the solver will escape the PISO loop. The tolerances defined inside the PIMPLE key word are requirements for the initial residuals at the start of each PISO loop. When the initial residuals fall below 1e-3, the solver will escape the PIMPLE loop and move onto a newer time step. The underrelaxation factors are unity in the final iteration, because a less-than-unity underrelaxation factor in the final iteration violates conservation of mass.

4 Likes
15

The following run.log best illustrates the PIMPLE algorithm. This output file comes from the LES validation of vortex shedding off a 3D cylinder in the simscale tutorial LES Validation from Simscale Documentation.What you can see is the final PIMPLE loop, which consists of 12 PIMPLE iterations. At the start of the first PISO loop ( the first PIMPLE iteration ), the residual of Ux is already 1e-4 and one PISO iteration drops this residual to 1e-8. Now the solver moves onto the next PISO loop ( the second PIMPLE iteration ). This time, only one PISO iteration was done to reduce the residual to 1e-8 as well. Twelve PISO loops ( PIMPLE iterations ) were performed as is defined in the solver setting.

Note that I have distinguished ‘iteration’ and ‘loop’ here to explain the PIMPLE algorithm, but in reality these two words are interchangeable.

Time = 8.99973674376
PIMPLE: iteration 1
DILUPBiCG: Solving for Ux, Initial residual = 0.000148508819129, Final residual = 7.44603976725e-08, No Iterations 1

PIMPLE: iteration 2
DILUPBiCG: Solving for Ux, Initial residual = 4.56830551041e-05, Final residual = 2.32563765734e-08, No Iterations 1

PIMPLE: iteration 3
DILUPBiCG: Solving for Ux, Initial residual = 1.6090038801e-05, Final residual = 7.44834114402e-09, No Iterations 1

PIMPLE: iteration 4
DILUPBiCG: Solving for Ux, Initial residual = 7.52783859765e-06, Final residual = 7.52783859765e-06, No Iterations 0

PIMPLE: iteration 5
DILUPBiCG: Solving for Ux, Initial residual = 4.37603976399e-06, Final residual = 4.37603976399e-06, No Iterations 0

PIMPLE: iteration 6
DILUPBiCG: Solving for Ux, Initial residual = 2.75251588942e-06, Final residual = 2.75251588942e-06, No Iterations 0

PIMPLE: iteration 7
DILUPBiCG: Solving for Ux, Initial residual = 1.76635756565e-06, Final residual = 1.76635756565e-06, No Iterations 0

PIMPLE: iteration 8
DILUPBiCG: Solving for Ux, Initial residual = 1.14109848252e-06, Final residual = 1.14109848252e-06, No Iterations 0

PIMPLE: iteration 9
DILUPBiCG: Solving for Ux, Initial residual = 7.40622832416e-07, Final residual = 7.40622832416e-07, No Iterations 0

PIMPLE: iteration 10
DILUPBiCG: Solving for Ux, Initial residual = 4.82898792766e-07, Final residual = 4.82898792766e-07, No Iterations 0

PIMPLE: iteration 11
DILUPBiCG: Solving for Ux, Initial residual = 3.16342215105e-07, Final residual = 3.16342215105e-07, No Iterations 0

PIMPLE: iteration 12
DILUPBiCG: Solving for Ux, Initial residual = 2.97479128819e-07, Final residual = 2.97479128819e-07, No Iterations 0

A lot of PIMPLE iterations are wasted in this particular simulation, as Ux is no longer solved after three PIMPLE iterations. If you look at the run.log in the validation, only pressure was still being solved in the 12th PIMPLE iteration. Also note that the pressure field is corrected (looks like solved here) twice because the PISO algorithm requires 2~3 pressure corrections performed. But the initial residuals of pressure at the start of each PISO loop are not considered low enough:

PIMPLE: iteration 1
GAMG: Solving for p, Initial residual = 0.706704526299, Final residual = 0.00341178806961, No Iterations 3
GAMG: Solving for p, Initial residual = 0.417801038703, Final residual = 0.00137080974962, No Iterations 4

PIMPLE: iteration 2
GAMG: Solving for p, Initial residual = 0.406367064313, Final residual = 0.0020114054495, No Iterations 3
GAMG: Solving for p, Initial residual = 0.254867385374, Final residual = 0.000859766460281, No Iterations 4

PIMPLE: iteration 3
GAMG: Solving for p, Initial residual = 0.242742425276, Final residual = 0.000775495113812, No Iterations 4
GAMG: Solving for p, Initial residual = 0.158851144936, Final residual = 0.000505381040559, No Iterations 4

PIMPLE: iteration 4
GAMG: Solving for p, Initial residual = 0.149588428163, Final residual = 0.000453812741632, No Iterations 4
GAMG: Solving for p, Initial residual = 0.100393977934, Final residual = 0.000294570683216, No Iterations 4

PIMPLE: iteration 5
GAMG: Solving for p, Initial residual = 0.0941553796383, Final residual = 0.000269934050947, No Iterations 4
GAMG: Solving for p, Initial residual = 0.0641894203528, Final residual = 0.000196821805463, No Iterations 4

PIMPLE: iteration 6
GAMG: Solving for p, Initial residual = 0.0601883940156, Final residual = 0.000178714012601, No Iterations 4
GAMG: Solving for p, Initial residual = 0.0414341714058, Final residual = 0.000137304405945, No Iterations 4

PIMPLE: iteration 7
GAMG: Solving for p, Initial residual = 0.0389232148202, Final residual = 0.000123383791728, No Iterations 4
GAMG: Solving for p, Initial residual = 0.0269592452001, Final residual = 9.65719245869e-05, No Iterations 4

PIMPLE: iteration 8
GAMG: Solving for p, Initial residual = 0.025395393977, Final residual = 8.62920927719e-05, No Iterations 4
GAMG: Solving for p, Initial residual = 0.017658060837, Final residual = 6.8102322988e-05, No Iterations 4

PIMPLE: iteration 9
GAMG: Solving for p, Initial residual = 0.0166843945302, Final residual = 6.0707998577e-05, No Iterations 4
GAMG: Solving for p, Initial residual = 0.011629915282, Final residual = 4.81263792425e-05, No Iterations 4

PIMPLE: iteration 10
GAMG: Solving for p, Initial residual = 0.0110217868388, Final residual = 4.2853469558e-05, No Iterations 4 
GAMG: Solving for p, Initial residual = 0.00769540689882, Final residual = 3.41080045519e-05, No Iterations 4

PIMPLE: iteration 11
GAMG: Solving for p, Initial residual = 0.00731348998233, Final residual = 3.0379449571e-05, No Iterations 4
GAMG: Solving for p, Initial residual = 0.00511174509437, Final residual = 2.42557245496e-05, No Iterations 4

PIMPLE: iteration 12
GAMG: Solving for p, Initial residual = 0.687500048762, Final residual = 0.0030887941433, No Iterations 3
GAMG: Solving for p, Initial residual = 0.0192081339871, Final residual = 7.09502196624e-05, No Iterations 17

The reason why the pressure field is not converged within each time step is because there is a relative tolerance set for pressure:

Usually this relative tolerance is set to zero for transient computation to force residuals to drop as much as possible, and therefore less PIMPLE iterations performed.

A more satisfactory residual plot (PIMPLE algorithm ) will look something like this:

Note that this is only a two-dimensional flow, and the exact orders of magnitude for the residual reduction within each time step of different parameters are still open to discussion/flow-field dependent.

2 Likes
16

Hi, if the initial pressure residuals do not change much, it probably is because the pressure field is no longer solved. Please see my previous posts on this matter.

17

@dylan - great posts, thanks a lot for sharing!

18

Is it possible to see the convergence plot as a function of iteration instead of time step, like @rarrese suggested, and @dylan used in his example?

19

Hi @mtree22, I believe they are the same in steady state. In transient state, you might need to download the results and plot residuals offline to get iterations on the x axis. I am not yet aware of anything on the platform to change the x axis.

Correction: the results for you to download don’t come with the run log so you can’t plot it offline.