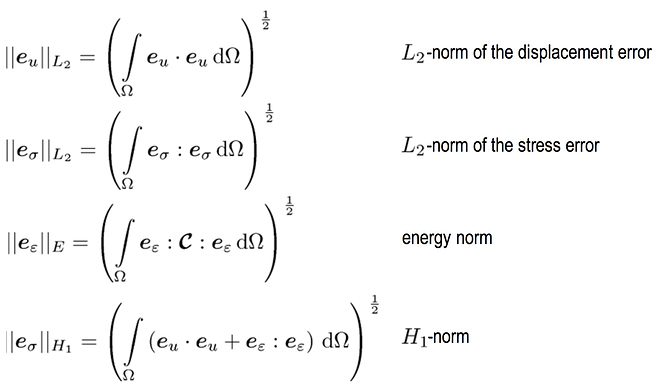If you want to know more about convergence, please first read our article about FEA where we have one paragraph dedicated to mesh convergence.
The first way to evaluate if a solution has converged would be to compare with analytical solutions or experimental results.
Error of the displacements:
where u is the analytical solution for the field.
Error of the strains:
where \epsilon is the analytical solution for the strain field.
Error of the stresses:
where \sigma is the analytical solution for the stress field.
As shown in the equations above, several errors can be defined for displacement, strains and stresses. These errors could be used to compare and they would need to reduce with mesh refinement. However, in a FEA mesh, the quantities are calculated at various points (nodal and Gauss). So in this case, where and at how many points should the error be calculated?
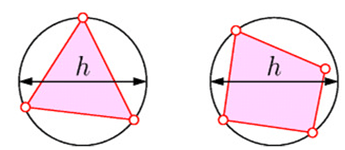
Figure 1
Alternatively, norms are defined such that the averaged errors over the entire structure or part of the structure can be calculated. Error norms can also be compared to the size of the element. Here “c” is a constant of proportionality while “h” is the element size, as defined in the figure above. Hence, several errors like L^2 and energy error norms can be defined as illustrated below:
However, in real practical applications, a non-dimensional version of the same is more useful to assess the actual degree of error. Hence, here the root-mean-square value of the norms as defined below is used to plot the reduction in error.
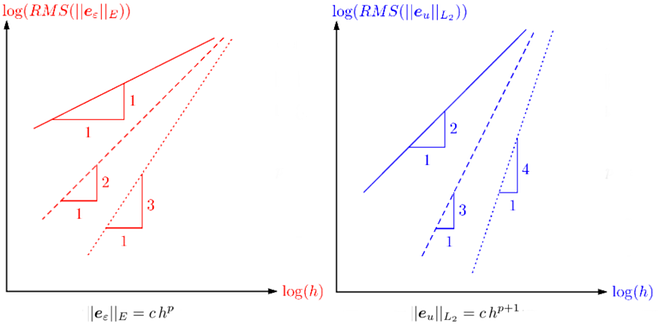
The final topic considers at what rates these errors ideally decrease. If we are using linear, square or cubic elements, how can be judged if the error is decreasing at the right speed or quality of algorithms coded? As shown in the picture below, the L^2-norm error decreases at the rate of p+1 and energy-norm at the rate of p.
Figure 2
Please visit our SimWiki article about FEA to find out more about convergence.