The project involves testing out of the various numerical settings in the incompressible analysis of airfoil.
When i set the value of all the relaxation parameters to 0.7, the simulation run ends with a floating point exception error. My initial values for the turbulence parameters are set to a non-zero value. The solver used for pressure is PCG and numerical schemes are predominantly linear. A sharp change in the residual of K is observed before the error.
The template of the project is based on Reference
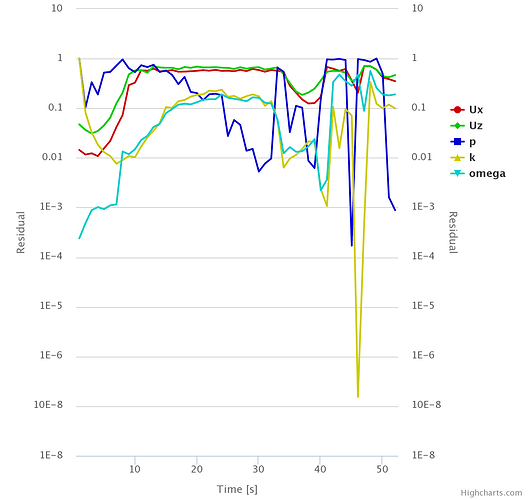
The convergence plot is as shown below
I would like to know what results in the floating point exception error and what would be the possible corrections to my simulation.
Regards
Aravind Baskar
Hi Aravind (@aravindbaskar) and thanks for the very detailed description of the problem!
This issue has already been discussed in some posts. I would recommend having a look at the following post from @jprobst: Floating Point Exception Error
Maybe you can get anything out of it and it will help your simulation. If not please let me know and I will try to figure out another solution.
Cheers and good luck!
Jousef
Hi @aravindbaskar, if you are experimenting with relaxation factors then this is the answer to one of your questions (presuming you model is well set up in terms of boundary conditions). Q: ‘What happens if I increase all relaxation factors to nearly 1?’ A: Instablity occurs. Reducing the relaxation makes convergence take longer but also reduces the instability caused by an incorrect value in the calculation.
So in summary, if you reduce your relaxation value you should get convergence. However, if not, you might wish to look at your setup (or share a project link here).
Kind regards,
Darren
1 Like
Exactly, @1318980 - This project is part of the CFD Master Class (Session 2) which focuses on Investigating the Impact of Numerical Settings.
Thus, @aravindbaskar - your setup is not wrong  Just have in mind how the stability and speed of the results vary with each different numerical configuration.
Just have in mind how the stability and speed of the results vary with each different numerical configuration.
Cheers,
Anna
1 Like
 Just have in mind how the stability and speed of the results vary with each different numerical configuration.
Just have in mind how the stability and speed of the results vary with each different numerical configuration.