It is quite common in simulation industry to associate FEA to structural analysis and CFD to fluid dynamics applications. This may be used in an industrial environment in day to day basis but that doesn’t mean it is true.
An example of CFD simulation
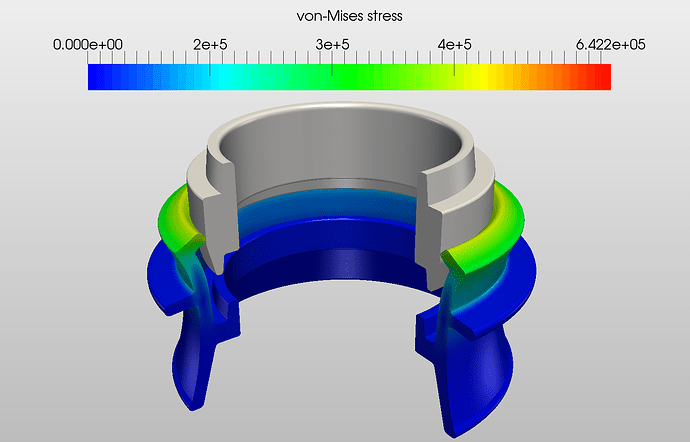
An example of FEM simulation done on Rubber seal
The Difference
The true difference will be clear once we expand the acronym. FEA/FEM stands for Finite Element Analysis/Method while CFD stands for Computational Fluid Dynamics. Now, it is clear that the former refers to a method while the latter refers to an application. FEM is a numerical method just like finite volume, finite difference and spectral method which are used for solving partial differential equations.
When a user refers to a CFD simulation, he implictly means fluid dynamics simulation using Finite Volume Method. It is very important to understand that one can also perform CFD simulations using FEM or any other method, but this is not as common as FVM. Infact, almost all the popular commercial and open-source codes such as Fluent, Open FOAM use FVM as their solving procedure.
Why FEM for fluids and FEM for solids?
The main reason why FVM is used for CFD is because of the fact that the governing equations for fluids i.e. Navier stroke’s equations have a non linear convection term which makes the problem unsymmetric and the standard FEM which is based on Bubnov-Galerkin formulation ( same shape functions for test and interpolation) fails without the stabilisation term. On the other hand, FVM which is based on conservation laws can handle this unsymmetry without the need of stabilisation term and has inherent local conservative property in the formulation. This is the main reason why it is preferred for solving fluid problems among the simulation community and hence FVM and CFD are used interchangeably.
Navier–Stokes equation in 2 dimension
FEM, on the other hand is very successful in the solid mechanics problems where the equations are self-adjoint elliptic (or symmetric) and thus standard FEM which is based on Bubnov-Galerkin becomes an ideal candidate for solving this class of problems. The method is so successful that it is synonymous to structural analysis and causing the confusion that exist today.