Coefficient of lift for a flow around a rotating cylinder

Project Support
1

Hey !!

Please go through the following project, and let me what exactly did I miss.

AIM:
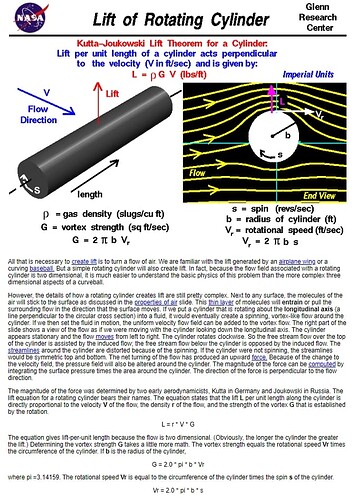
Trying to validate the case of Kutta-Joukowski theorem for the flow around a 2D rotating cylinder.
For my project, following are the specifications,
Radius =0.2m, density =1 kg/m^3, kinematic viscocity = 0.02,
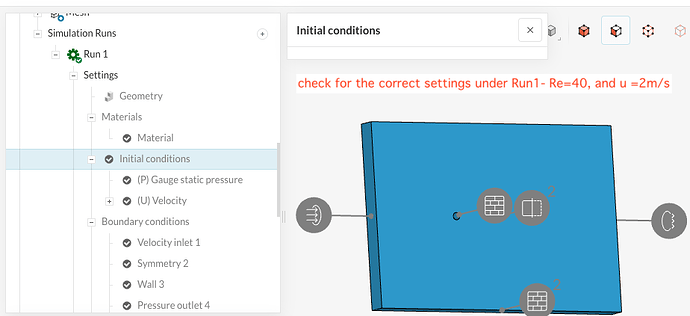
Consider the first case for Re=40, i.e, incoming velocity =2 m/s. Here I calculated spin velocity as spin vel = incoming vel/ radius =10.

As per the theorem,

  • circulation = 2piRadius^2 * spin velocity(rad/sec)
    *Coeff of lift = circulation / (radius x flow velocity)
    *Lift per span= density(=1 kg/m^3)x flow velocity x circulation

However, the coefficient of lift value which I am getting is different from what is expected.
I have used laminar steady model. However, I also tried with k-omega sst, and laminar unsteady too. However, all are giving almost the same results. I am doing some mistake in the simulation set up.

I rechecked the directions(axis), and boundary conditions for each, and found all correct. I have no idea where am i going wrong. Can someone check the setup in the following section(as I have tried different set ups, which basically gives almost the same results. ):

ss
ss924×424 35.5 KB

Also, I tried lowering the spin velocity, as the spin and incoming velocity are independent of eachother, however, even there, the same thing is happening.

2

here is the link

3

Hi @athiram

Thanks for the project link. The lift coefficient seems to be reasonable for this setup as it is now, but I am not sure about this rotating wall BC for the cylinder. Which lift coefficient value are you reaching for?

Please, do you have something to point out @DaleKramer? In this meantime, maybe worth to take a close look at this simulation setup: Fluid Flow around a Cylinder with CFD by SamPrabhu | SimScale

best,

1 Like
4

Thankyou for the prompt response. With respect to the model simulation setup, I have already done a project for stationary cylinder, and I got the desired results. However, I am not sure if the laminar steady model would work for the flow around the rotating cylinder, despite setting a lower Reynolds number. I did try with other models, and ended up getting more or less similar results.

For the given specifications(as per the above formulae): i.e, spin vel=10, inco vel =2, radius =0.2
circulation = 2.513
Lift = 5.02 N
Coeff of lift = 6.28, and I am getting nothing close to it.

5

Sorry, I do not have much experience with rotating wall boundary conditions but I did have a look at the project.

And I even played with this NACA applet : Curve Ball Pitch Interactive | Glenn Research Center | NASA

What surprised me with the applet is how many rpm the ball needs to have to appreciably affect a pitched baseball .

With this in mind I am confused that the ‘spin vel’ of 10 is required in 1st post but the sim setup uses 0.1 rad/sec . Could the issue be simply a ‘units’ error on spin velocity?

1 Like
6

Hey!!

Since I tried the simulation set up by changing the input parameters, you must have mistook the wrong set up. I was referring to the one with the title ‘Re=40 and u=2m/s’.

Is there anything wrong with my implementation of the domain or boundary conditions?

7

Yes I just looked at the last run in the last simulation.

Domain and boundary conditions looked OK but you may have changed them by the time I looked at it.

Sooo, when asking for help, please gives us a link to the results and or simulations that you are questioning AND in addition it is helpful if you stop playing with that specific simulation until things are resolved. If you want to continue to work on the project just copy the whole simulation and work on the copy.

Do I take it from this that ‘vel’ would be in meter/sec and ‘radius’ is in meters which gives units for your division to be 1/sec. How is that radians/sec?

Also I believe there may be something wrong with the values for the parameters for your coefficient calculations. Your Lift/Drag value of 2.75 does not match the value of CL/CD which is 1.86 (I think…)

Here is an example of a link to your ‘Forces’ output of 'Run 1 ’ for Simulation ‘Re=40 and u=2m/s’ (in the copy I made of your project)
:
https://www.simscale.com/workbench/?pid=4920690322845129105&rru=27b39b62-084d-4d53-8ed5-1f71ad644baa&ci=a7a66c76-ac1e-4661-a651-84812a498fa6&ct=PLOT&mt=SIMULATION_RESULT

8

Dear Dale,

My sincere apologies!

Please refer to the above link for the results for the particular case of Re=40, u=2m/s.

Now about how I arrived at the results:

Radius =0.2m, density =1 kg/m^3, kinematic viscocity = 0.02,
For Re=40, i.e, incoming velocity =2 m/s. Here I calculated spin velocity as spin vel = incoming vel/ radius =10 rad/s. I know your question makes sense about the units. Please refer to : Lift of a Rotating Cylinder, for a general explanation. I do not know how to explain better from my end. In the simulation set up, I have used SI units.

According to the Kutta-Joukowski theorem:
*** circulation = 2piRadius^2 * spin velocity(rad/sec)**
*** Lift per span= density(=1 kg/m^3)x flow velocity x circulation**
*** Coeff of lift = circulation / (radius x flow velocity)**

So in this case, expected values are :
[not including the units as it is all in SI]
Circulation = 2.5132, Lift = 5.026, and Cl = 6.2831.

Whereas, the obtained values from simulation is:
Lift = Total Force_y = 2.1330 N
Drag =Total Force_z =1.135 N( flow direction is along Z)
L/D = 1.87
Coefficient of lift = 2.666
Coefficient of drag = 1.4191
L/D = 1.87

Based on these values, applying the inverse formula to calculate the circulation, we will get circulation = 1.064

I have no idea if I am making any mistakes in doing anything related to rotation parameters. The cylinder is expected to rotate in the clockwise rotation in y-z plane(i.e. with respect to the incoming flow(along Z axis) towards 0–>z, applying the right hand rule, spin direction will be set along +X axis.

I did the same implementation for stationary cylinder, and it worked, I have no idea what is going wrong here.

9

Sorry but I am still stuck on the proper rad/sec to use in the simulation parameter for ‘w’ (omega) , in your reference (shown below they use ‘s’ which is in revs/sec.

From now on lets talk only the symbols in the equations here:

Lift of a Rotating Cylinder
Lift of a Rotating Cylinder674×946 130 KB

For your expected values, can you specify the value of each input variable and show your recalculations of your expected values?

11

As far as your mesh and simulation parameters are concerned with regard to ‘best CFD practices’ for your projects purpose:

  1. I am concerned that you choose a Laminar Turbulence model for the simulation ‘Re=40 and u=2m/s’. With a Laminar turbulence model you are not able to specify that the Solver calculate a yPlus surface mapping for the results generated. I would use the ‘k-omega SST’ turbulence model for the simulation and then specify, in the Results control>Field Calculations tree item, the Turbulence parameter which will generate your yPlus mapping.

  2. Since Mesh 3 was deleted at the time I made my copy of your project I can not look at its meshing log which would really help me to comment on the quality of Mesh 3 which was used in your Run1 of the Simulation ‘Re=40 and u=2m/s’

Until I see a meshing log for the mesh you use in a simulation that you question the results for and a yPlus surface mapping, I can not further debug whether you have used ‘best CFD practices’ for the results that you have concerns about.

I think you will need to do another Simulation with a successful Run to proceed.

And remember:

12

Continuing the discussion from Coefficient of lift for a flow around a rotating cylinder:

Re=40

Radius =0.2m =0.656168(ft),

density =1 kg/m^3 =0.00194032(slugs/cu ft)

incoming velocity =2 m/s = 6.56168 (ft/sec).

Spin = 1.59 rev/sec

Rotational Velocity= 10 rad/sec =2 m/sec (for this case R=0.2m) = 6.56ft/sec

According to the Kutta-Joukowski theorem:

  • circulation = 2piRadius^2 * spin velocity

  • Lift per span= densityx flow velocity x circulation

  • Coeff of lift = circulation / (radius x flow velocity)

So in this case, expected values are :

  • Circulation = 2.5132 (SI) = 27.0518597(sq ft/sec),
  • Lift per unit span= 0.3441 slug /(ft sec) =11.07109 (lbs/ft)

There were few conversion in the lift part , and I missed it, and thus had to delete the previous reply.

I will perform a new simulation for the most simple case, and then send the results in SI units, as it is standard and more easy to talk in terms of.