Documentation
This validation case belongs to vibrations and the elastic support boundary condition in solid mechanics. The aim of this test case is to validate the following parameters:
The simulation results of SimScale were compared to the results derived from [Schaum]\(^1\).
The geometry used for the case is as follows:
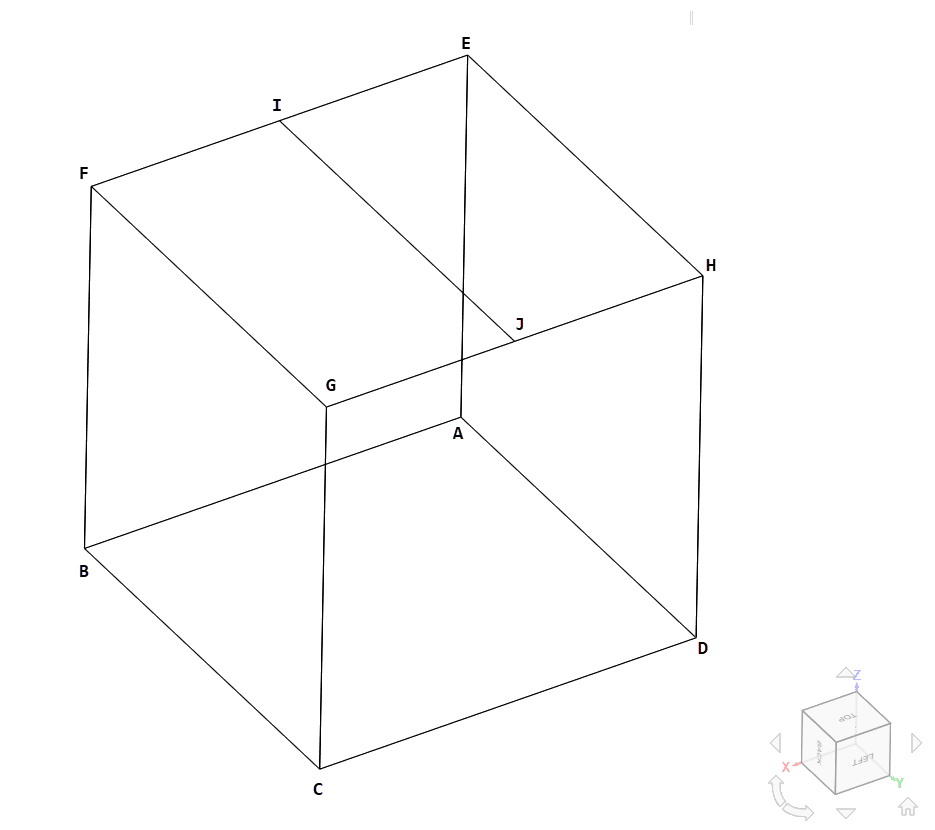
The cube has an edge length of 1 \(m\), with the upper face partitioned in half.
Tool Type: Code Aster
Analysis Type: Static Linear and Dynamic
Cases corresponding to analysis type are as follow:
| Case | Analysis Type |
|---|---|
| A-1 | Static Linear |
| A-2 | Dynamic |
| B-1 | Static Linear |
| B-2 | Static Linear |
| B-3 | Static Linear |
Mesh and Element Types:
Tetrahedral meshes were computed using SimScale’s standard mesh algorithm and manual sizing.
| Case | Mesh Type | Number of Nodes | Number of Elements | Element Type |
|---|---|---|---|---|
| A-1 | 1st Order Tetrahedral | 45 | 97 | Standard |
| A-2 | 1st Order Tetrahedral | 45 | 97 | Standard |
| B-1 | 1st Order Tetrahedral | 128 | 405 | Standard |
| B-2 | 1st Order Tetrahedral | 128 | 405 | Standard |
| B-3 | 1st Order Tetrahedral | 128 | 405 | Standard |

Material:
Boundary Conditions:
The following table summarizes the elastic support boundary conditions by case:
| Case | Elastic Support Type on Face EIGJ | Elastic Support Type on Face IFJH | Elastic Support Type on Face EFGH |
|---|---|---|---|
| A-1 | – | – | Isotropic Total |
| A-2 | – | – | Isotropic Total |
| B-1 | Isotropic Total | Orthotropic Total | – |
| B-2 | Isotropic Distributed | Orthotropic Distributed | – |
| B-3 | Isotropic Total+Distributed | Orthotropic Total+Distributed | Isotropic Total |
The analytical solutions for the rotation angle \(\theta_B\) and maximum shear stress \(\tau_{max}\) are given by the following equations:
Cases A-1, B-1, B-2, B-3:
\( x = \frac{mg}{k} \tag{1} \)
Case A-2:
\( x(t) = V_0 \omega Sin(\omega t) + X_0 Cos(\omega t) \tag{2} \)
\( \omega = \sqrt{ k / m} \tag{3} \)
\( V_0 = -0.01 m/s \)
\( X_0 = -0.02 m \)
\( X_eq = -0.01 m \)
\( 2 <= t <= 4 \)
The computed reference solution is:
\( x_{static} = 0.01\ m \)
\( \omega = 31.32\ Rad/s \)
\( x(t) = (-3.193*10^{-4})Sin(31.32t) – 0.01Cos(31.32t) \tag{4} \)
*\( x(t) \) corresponding to the displacement with respect to the equilibrium position.
Comparison of displacement DZ on static cases:
| CASE | DZ | REF | ERROR |
|---|---|---|---|
| A-1 | 0.01 | 0.01 | 0 % |
| B-1 | 0.01 | 0.01 | 0 % |
| B-2 | 0.01 | 0.01 | 0 % |
| B-3 | 0.01 | 0.01 | 0 % |
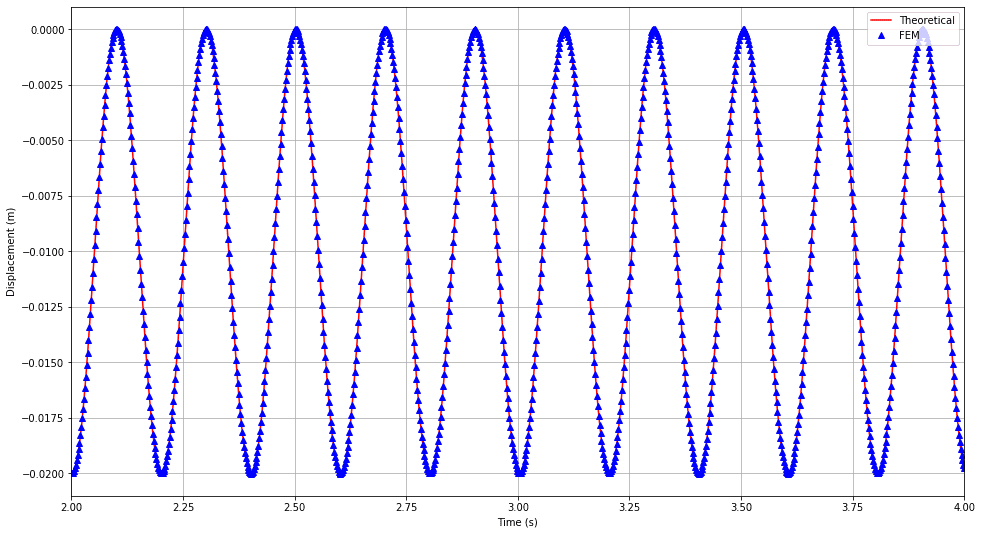
Comparison of transient displacement of face ABCD in dynamic case can be found in Figure 3. Here the vibrations from the elastic support condition can be appreciated.
References
Note
If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.
Last updated: October 8th, 2020
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now