Warning
A constant non-zero boundary condition was defined for a nonlinear analysis. Please consider to always ramp your load using a formula or table value in order to ease convergence – otherwise the automatic time stepping will not have any effect on the convergence and your simulation might fail.
What Happened?
This is a warning message which points out that there is a non-zero constant boundary condition in nonlinear analysis. This can be a constant load or a constant displacement. This message warns the user to avoid doing this in order to allow the solution to converge more easily.
What Could Be the Possible Reason?
For nonlinear analysis, where geometric or material nonlinearities are expected to be present, a constant boundary condition may introduce high nonlinearities that cannot be resolved correctly. At each time step, the same equation system will be solved. This means that the solver will try to solve for a high load in the first time step and will most probably fail to converge. If auto timestep definition is used, the solver will try to reduce the nonlinearity by breaking the time steps into smaller ones but this has no effect and the simulation will fail to converge.
What Can I Do Now?
A good practice is to ramp the load or displacement either by using a function or table upload. For example, one of the tutorials that we have is a nonlinear analysis of a wheel. The load is applied downward in the negative z-direction.
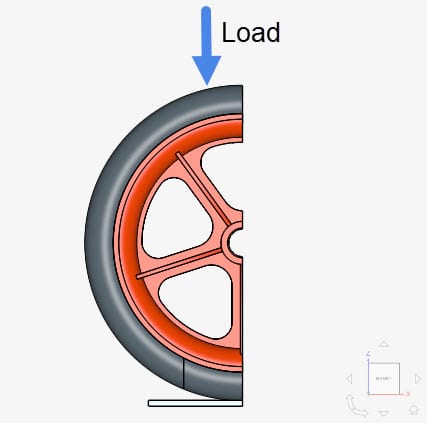
In the simulation setup, you can see that the load is not constant throughout the simulation, but varies over time where the load at 0.5 \(s\) is 1000 \(N\) and at 1 \(s\) is 500 \(N\).

Important Information
If none of the above suggestions solved your problem, then please post the issue on our forum or contact us.